Recently, a friend of mine from Turkey who is writing his Ph. D. on a chess theme asked me how many types of players chess people are? Since I did not know what precisely to asnwer, I decided to publish his study, so that anyone who is interested in this subject can answer him, and discuss the topic. Here it comes:
From Necati Alp ERİLLİ1
1Statistics Dep. / Faculty of Science / 19 May Univ. / Samsun
E-mail address: aerilli@omu.edu.tr
ABSTRACT – Chess is the most popular brain game in the world. Since it has been playing for centuries, we have usually met the same questions typically: “Who is the strongest player in the world?, Can you beat me?, What’s your style?” It is hard to answer these types of questions which need objectivity. Every chess game has an ECO code. These codes help players for preparing to opponents or improving themselves. We classify chess players according to their styles by using ECO codes. These codes are named by A to E capitals and numbers from 00 to 99. In general there are 500 different types of chess openings. Some openings are aggressive and some are defensive. These codes are in crisp data form but results can be in crisp or fuzzy data form. By using fuzzy clustering analysis we can classify players into 3 groups. They are; aggressive player, defensive player or positional player. Results have been tested on some strong players and some amateur players. All these show that we can use fuzzy systems in these complicated problems.
Keywords: Fuzzy Clustering, ECO Codes, Chess, Fuzzy Data
Introduction
Chess is the most popular brain game in the world. It is a board game played between two players. It is played on a chessboard, which is a square-checkered board with 64 squares arranged in an eight-by-eight grid. At the start, each player controls sixteen pieces: one king, one queen, two rooks, two knights, two bishops, and eight pawns. The object of the game is to checkmate the opponent's king, whereby the king is under immediate attack (in "check") and there is no way to remove or defend it from attack on the next move.
In recent years chess became more popular than previous centuries by the help of FIDE (World Chess Federation), chess lessons in schools and World Championship games. Chess not only develops memory, logical thinking, capability but also improves concentration and teaches independence [1]. Chess has long been considered a way for children to increase their mental prowess, concentration, memory and analytical skills. To anyone who has known the game, it comes as no surprise that these assumptions were actually proven in several studies on how chess can improve the grades of students [2].
The main problem for chess players is their graduates. For ranking players a mathematical system called ELO has been introduced by Hungarian Mathematician Dr. Arpat Elo. It has been using since 1970. World Chess Federation expresses ELO list in every three months. By this list, players listed in order to their elo points in tournaments. Players can learn their world ranking or country rankings through this list.
Another point for chess players is their positions among all of the players. It is hard to make a decision for players which category they in. Good player or bad player or defensive players etc. are all linguistic expressions. All they are subjective and can be change for everyone.
In this article we try to classify players whether they are defensive player, aggressive player or positional player. The names are co-decision thanks to chess players around us.
We utilize from ECO codes to classify players. Every chess game has an opening code called ECO code. Every move has a typical task for openings. Some openings ended 6 or 7 moves and some openings ended 20 or 25 moves. Some of them called openings and some of them called defence for names in private. ECO codes are named by A to E capitals and numbers from 00 to 99. In general there are 500 different types of chess openings. These codes are in crisp data form. But we use them as fuzzy data for estimation.
We classify players looking to their game scores and game ECO codes. After a game finishes player can take 1 point for victory, 0,5 point for draw and 0 point for loss. By using these codes and scores which had been taken in games, we can put them in to classes which we determine at the beginning.
With the help of Fuzzy clustering analysis we can classify players into groups which we determined in the beginning.. It is one of the common technique in statistical classification methods.
FUZZY CLUSTERING
Cluster analysis is a method for clustering a data set into groups of similar objects. It is an approach to unsupervised learning and also one of the major techniques in pattern recognition [3]. Hard clustering methods allow each point of the data set to exactly one cluster. Zadeh [6] proposed fuzzy sets that can use for the idea of partial membership described by a membership function. After that many fuzzy clustering methods have been studied [4,5,7,8,14].
Fuzzy Cluster Analysis of Crisp Data
This approach comes into the picture as an appropriate method when the clusters cannot be separated from each other distinctly or when some units are uncertain about membership. Fuzzy clusters are functions modifying each unit between 0 and 1 which is defined as the membership of the unit in the cluster. The units which are very similar to each other hold their places in the same cluster according to their membership degree.
Similar to other clustering methods, fuzzy clustering is based on distance measurements as well. The structure of the cluster and the algorithm used to specify which of these distance criteria will be used. Some of the convenient characteristics of fuzzy clustering can be given as follows [10]:
i. It provides membership values which are convenient to comment on.
ii. It is flexible on the usage of distance.
iii. When some of the membership values are known, they can be combined with numeric optimization.
The advantage of fuzzy clustering over classical clustering methods is that it provides more detailed information on the data. On the other hand, it has disadvantages as well. Since there will be too much output when there are too many individuals and clusters, it is difficult to summarize and classify the data. Moreover, fuzzy clustering algorithms, which are used when there is uncertainty, are generally complicated [13].
In fuzzy clustering literature, the fuzzy c-means (FCM) clustering algorithm is the most well-known and frequently used method. FCM is a method of clustering which allows one piece of data to belong to two or more clusters. This method which is developed by Dunn [9] and improved by Bezdek [11], is frequently used in pattern recognition. It uses Euclidean distance between variables and cluster centers:
d_ik=d(x_i,v_k )=[∑_(j=1)^p▒(x_ji-v_jk )^2 ]^(1/2)
(1)
It is based on minimization of the following objective function:
J(u,v)=∑_(j=1)^n▒〖∑_(k=1)^c▒〖u_jk〗^m ‖x_ji-v_jk ‖^2 〗
(2)
Here; m is any real number greater than 1, u_jk is the degree of membership of x_i in the cluster j, x_i is the i’th of d-dimensional measured data, v_j is the d-dimension center of the cluster, and ||*|| is any norm expressing the similarity between any measured data and the center.
Fuzzy partitioning is carried out through an iterative optimization of the objective function shown above, with the update of membership u_ik ;
u_ik=[∑_(j=1)^c▒(〖d_ji〗^ /〖d_jk〗^ )^(2/(m-1)) ]^(-1)
(3)
and the cluster centers v_jk by:
v_jk=(∑_(j=1)^n▒〖u_jk^m x_ik 〗)/(∑_(j=1)^n▒u_jk^m )
(4)
1≤j≤c , 1≤i≤n
Equations (3) and (4) constitute an iterative optimization procedure. The goal is to iteratively improve sequence of sets of fuzzy clusters until no further improvement in J_m is possible.
The FCM algorithm is executed in the following steps:
Step 1: Initialize the following values: Number of cluster c, value of fuzziness m, termination criterion (threshold) ε and membership matrice U. Here, ε takes degree between 0 and 1.
Step 2: Calculate the fuzzy cluster centroid v_jk for i=1,2,…,c using (4).
Step 3: Employ (3) to update fuzzy membership u_ik.
Step 4: If the improvement in J_m is less than a certain threshold (ε), than halt; otherwise go to step 2.
Fuzzy Cluster Analysis of Fuzzy Data
Cluster analysis constitutes the first statistical area that lent itself to a fuzzy treatment. The fundamental justification lies in the recognition of the vague nature of the cluster assignment task. For this reason, in the last 3 decades, many fuzzy clustering models for crisp data have been suggested as we mentioned.
The fuzzy clustering of fuzzy data has been studied by different authors [20]. Sato and Sato [12] suggest a fuzzy clustering procedure for interactive fuzzy vectors. Yang and Ko [15] proposed clustering model called “Double fuzzy K-numbers clustering model” which deals with a single fuzzy variable on l units. “Fuzzy K-means clustering model for conical fuzzy vectors” proposed by Yang and Liu [16] is applicable to multi-dimensional fuzzy variables observed on l units. Yang et al. [17] proposed a clustering model called “Fuzzy K-means clustering model for mixed data” to classify mixed data like symbolic data or LR-II type data. Hung and Yang [18] proposed a clustering model called “Alternative double fuzzy K-means clustering model” to classify units. Authors used an exponential type distance for LR fuzzy numbers based on the idea of Wu and Yang [19] and discussed the robustness of this distance.
III. DOUBLE FUZZY K-NUMBERS CLUSTERING MODEL
This clustering model proposed by Yang and Ko [15]. It is assumed that the membership function of the fuzzy variable belongs to LR family and the univariate fuzzy data are represented by W_i=〖(m_(W_i ),α_(W_i ),β_(W_i ))〗_LR . Here m is called the mean value of W_i and α and β are called the left and right spreads, respectively.
The authors suggested a distance measure each pair of fuzzy numbers X_jand W_i as follows.
d_LR^2 (X_j,W_i )=1/3 {〖(m_(X_j ) 〖-m〗_(W_i ))〗^2+〖((m_(X_j ) 〖-α〗_(X_j ) )-(m_(W_i ) 〖-α〗_(W_i ) ))〗^2+〖((m_(X_j ) 〖+β〗_(X_j ) )-(m_(W_i ) 〖+β〗_(W_i ) ))〗^2 } (4)
Objective function is given as follows:
J_FCN (μ,W)=∑_(j=1)^n▒∑_(i=1)^c▒〖μ_i^m (X_j ) d_LR^2 (X_j,W_i ) 〗
(5)
Here m>1 is the index of fuzziness and μ=(μ_1,…,μ_c) is a fuzzy c-partition and W_i=〖(m_(W_i ),α_(W_i ),β_(W_i ))〗_LR are fuzzy c-numbers of LR-type. The necessary conditions for minimize (μ,W) of J_FCN are the following update equations:
m_(W_i )=(∑_(j=1)^n▒〖μ_i^m (X_j )[3m_(X_j )+(α_(W_i )-α_(X_j ))+(β_(X_j )-β_(W_i ))〗)/(3∑_(j=1)^n▒〖μ_i^m (X_j)〗)
i=1,…,c (
6)
α_(W_i )=(∑_(j=1)^n▒〖μ_i^m (X_j )[m_(W_i )-m_(X_j )+α_(X_j )]〗)/(l∑_(j=1)^n▒〖μ_i^m (X_j)〗)
i=1,…,c (
7)
β_(W_i )=(∑_(j=1)^n▒〖μ_i^m (X_j )[m_(X_j ) 〖-m〗_(W_i )+β_(X_j )]〗)/(r∑_(j=1)^n▒〖μ_i^m (X_j)〗)
i=1,…,c (
8)
and
μ_i^m (X_j )=〖[1/(d_LR^2 (X_j,W_i ) )]〗^(1/(m-1))/(∑_(k=1)^c▒〖[1/(d_LR^2 (X_j,W_k ) )]〗^(1/(m-1)) )
i=1,…,c ; j=1,…,n (9)
IV.APPLICATION
By using DFKC we try to classify chess players in to clusters according to their style.
There are lots of chess styles according to chess players from amateur to top players. There can be many answers for the question of chess style. We simply categorized players in to 3 clusters: Defensive players, Aggressive players and positional players. Defensive players generally use defensive openings in which colour they are. Their scores depend on their defensive power during games. Aggressive player use sharp opening both in white and black. They use open openings for winning the game immediately. Positional players use the openings according to their opponents. Sometimes they use sharp openings sometimes they use defensive openings to hold the game in safe.
The authorities categorized chess openings in to 6 sub categories. This classification is not official but many people accept that in general use. We can classify openings in to 6 clusters: Open (Starts with 1.e4 e5), Closed (Starts with 1.d4 d5), Semi-Open (1.e4 (without e5)), Hint Systems (1.d4 Nf6), Wing Systems (Generally starts with a, b, c or f pawns) and Other openings (Not grouped to previous ones).
As we stated every chess game has an Eco code. This simple code gives information for the opening. In which category it belongs, its name and its sub-level.
For example B20 to B99 named as Sicilian Defence. But in detail B33 named as Sveshnikov Variation, B44 Taimanov System and B50 Kopec Variation etc.
Numerical Example
Our first player is former World Chess Champion Garry Kasparov. Results have been taken from his best games in his career [21]. Firstly Kasparov’s results had listed according to their Eco codes. Then every sub-Eco code counted as a fuzzy number. For example A0 counted as LR-type fuzzy number (2.33, 1.33, 0.01). Here numbers are mean, left spread and right spread respectively. Every player has games both white and black. So we calculated results for white and black separately. For example Kasparov’s results in white for A and B openings are given below:
Table 1-Fuzzy Numbers for Kasparov in A and B Op.
Mean Left Right Mean Left Right
A0 2,33 1,33 0,01 B0 3 0,01 0,01
A1 2,6 0,8 0,01 B1 2,5 1 0,01
A2 2,28 0,85 0,14 B2 NAN NAN NAN
A3 2,5 1 0,01 B3 2,36 0,91 0,91
A4 3 0,01 0,01 B4 2,36 0,91 0,91
A5 2,33 1,33 0,01 B5 2 2 0,01
A6 3 0,01 0,01 B6 2,28 0,28 0,28
A7 3 0,01 0,01 B7 2,66 0,66 0,01
A8 2 2 0,01 B8 2,63 0,72 0,01
A9 3 0,01 0,01 B9 2,42 1,14 0,01
Figure 1-Seperation draw for Whites’ results
If we look to the figure 1, we can see cluster number is one for white results. Similarly black results are nearly same either. There is only one outliner in the figure but that opening played only 2 times. It isn’t necessary to take it calculate for clustering.
Figure 2-Three style for a particular criterion
We know that fuzzy sets are suited to describing ambiguity and imprecision in natural language and we may thus define these terms using triangular fuzzy numbers as follows:
X_Defensive=(0;0;1,5);〖 X〗_Positional=(1,5;1,5;1,5) X_Aggressive=(3;1,5;0)
These representations are shown in figure 2.
According to Kasparov’s games results, nearly every opening scores gets between 2 and 3. His average in white pieces (2,43; 0,71; 0,06) and in black pieces (2,42; 0,81 ;0,21). His scores generally equal to aggressive in all openings. As a result we can surely say that Garry Kasparov is an aggressive player both in white and black pieces.
Top players of the world chess are belong to aggressive class. This score are expected as well. New world chess champion V.Anand’s average is (2,41; 0,7 ;0,06) in white and (2,4; 0,99 ;0,06) in black or former world champion A.Karpov’s average is (2,426; 0,77 ;0,05) in white and (2,39; 0,88 ;0,066) in black. We can say both are aggressive during their careers.
Here are my scores from my career. I played 397 games which added to official tournaments. Results showed that I am aggressive player with white pieces and positional player with black pieces. In general I am between aggressive and positional player but nearest to aggressive side. But as addition i have to say that my opponents averages not same like top players as well.
Table 2-My scores to opening clusters
WHITE BLACK
Bird Positional Aggressive Sokolsky
English Aggressive Aggressive Queen-Indian
Queen Pawn Aggressive Positional Budapest
Holland Positional Defensive Pirc
Alekhine Defensive Positional Sicilian
Pirc Positional Aggressive French
Scilian Positional Positional Two Knight
French Aggressive Aggressive Queen Pawn
Philidor Aggressive Positional Gruenfeld
Petroff Aggressive Positional King-Indian
Ponziani Aggressive Positional Spanish
Two Knight Aggressive
Spanish Positional
Queen Gambit Aggressive
Queen-Indian Aggressive
My mean values are for white (2,24; 0,87; 0,78) and for black (1,91; 1,01; 1,28).
V.DISCUSSION
There are a lot of methods for fuzzy clustering in fuzzy data. Chess games or chess data never used in this kind of papers. We try to show that these type of irregular data can be used in clustering algorithms. Uses of these kind of data showed that, we can use much linguistic expressions in clustering methods.
VI.REFERENCES
[1] Dr. Robert C.Ferguson. Teacher’s Guide: Research and Benefits of Chess. (2006). (www.quadcitychess.com)
[2] Dean J. Ippolito. The benefits of chess in education. (2006). Benefits of chess for children. (www.deanofchess.com/benefits.htm)
[3] Rencher A.C.,(2002). Methods of Multivariate Analysis, John Wiley&Sons Inc.,UK.
[4] Bezdek, J.C., (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York.
[5] Dave, R.N., (1992). Generalized Fuzzy C-Shells Clustering and Detection of Circular and Elliptical Boundaries. Pattern Recognition 25 (7), 713-721.
[6] Zadeh, L.A., (1965). Fuzzy Sets, Inf. Control 8, 338-353.
[7] Gath, I., Geva A.B., (1989). Unsupervised Optimal Fuzzy Clustering. IEEE Trans. Pattern Anal. Machine Intell. 11, 773-781.
[8] Höppner, F., Klawonn, F., Kruse R., Runkler, T., (1999). Fuzzy Cluster Analysis: Methods for Classification Data Analysis and Image Recognition. Wiley, New York.
[9] Dunn J.C., (1974). A Fuzzy Relative of the ISODATA Process its Use in Detecting Compact Well-Separated Clusters, J. Cybernet. 3, 32-57.
[10] Naes T., Mevik T.H., (1999). The Flexibility of Fuzzy Clustering Illustred By Examples, Journal Of Chemo Metrics.
[11] Bezdek, J.C., (1981). Pattern Recognition with Fuzzy Objective Function Algorithms. Plenum Press, New York.
[12] Sato and Sato (1995). Fuzzy clustering model for fuzzy data. Proceedings of IEEE.2123-2128.
[13] Oliveira J.V., Pedrycz W., (2007). Advances In Fuzzy Clustering And Its Applications, John Wiley &Sons Inc. Pub.,West Sussex, England.
[14] Fukuyama Y., Sugeno M., (1989). A New Method Of Choosing The Number Of Clusters For The Fuzzy C-Means Method, Proceedings Of 5th Fuzzy Systems Symposium, pp 247-250.
[15] Yang M.S.and Ko C.H.(1996) on a class of fuzzy c-numbers clustering procedures for fuzzy data. Fuzzy sets and systems,84,49-60.
[16] Yang M.S. and Liu H.H.(1999). Fuzzy clustering procedures for conical fuzzy vector data. Fuzzy sets and systems, 106, 189-200.
[17] Hwang P.Y. and Chen D.H.(2004) Fuzzy clustering algorithms for mixed data feature variables, fuzzy sets and systems,141,301-317.
[18] Hung W.L. And Yang M.S.(2005). Fuzzy clustering on LR type fuzzy numbers with an application in Taiwanese tea evalution. Fuzzy sets and systmes, 150,561-577.
[19] Wu K.L. and Yang M.S. (2002) alternative c-means clustering algorithms. Pattern recognition, 35, 2267-2278.
[20] Oliveira J.V. and Pedrycz W., Advances in fuzzy clustering and its applications (2007). John Wiley & Sons Ltd.,West Sussex,England.
[21] Sahovski Informator 76, VI-IX (1999).
30.11.10
25.11.10
Amazing Resourcefulness
One Bulgarian GM won a silver medal on his board at the ECC in Plovdiv. He managed to win a couple of difficult games against players rated over 2650 as black. Although his result was in some way a piece of luck, it should not be underestimated. After all, luck should be searched, chased and only then deserved. Have a look at this remarkable game to see what I mean:
Naiditsch,Arkadji (2674) - Nikolov,Momchil (2549) [B42]
EU Plovdiv 2010 (4), 20.10.2010
[Momchil Nikolov]
1.e4 c5 2.Nf3 e6 3.d4 cxd4 4.Nxd4 a6 5.Bd3 Nf6 6.0–0 Qc7 7.Qe2 d6 8.c4 g6 9.Nc3 Bg7 10.Nf3 0–0 11.Rd1 Nc6 12.Bc2 Ng4 13.Ne1?!

13...f5?! [13...Nge5! 14.f4 Nd7 15.Nf3 Na5! 16.Bd3 Nb6! (16...b6=) 17.c5! dxc5 18.Be3 Nd7! 19.Rac1 c4 20.Bb1 b5 with good play] 14.h3 Nf6?! [14...Nge5 15.f4 Nf7 16.Nf3 Bd7=] 15.Nf3 Ne5 [15...fxe4 16.Nxe4 Nxe4 17.Bxe4 Ne5 is better for White] 16.Nxe5 dxe5 17.b3! Rf7 18.Ba3 Bf8 [18...Qa5 19.Na4 Bd7 20.b4 Qc7 21.Nc5±] 19.Bxf8 Rxf8 20.Qd2 Bd7 21.Qd6 Qxd6? [21...Rac8! 22.Rd3 a) 22.f4 exf4 23.e5 Nd5! This was the move that I missed while calculating the option: (21...Tac8!)- 24.Nxd5 (24.Qxc7 Rxc7 25.Nxd5 exd5 26.Rxd5 Re8) 24...exd5 25.Qxd5+ Rf7= 26.e6 Qb6+; b) 22.Rd2 b5!; 22...b5! 23.exf5 Qxd6 24.Rxd6 gxf5 25.Rxa6 bxc4 26.b4 Ra8=] 22.Rxd6 Kf7?! [22...Rad8? 23.Rad1 f4 (23...Kf7 24.f4!+-) 24.Na4+-; 22...Rae8!? 23.f4 Bc8! 24.fxe5 Nd7 25.Na4 Nxe5 26.Nb6±] 23.f4! Bc6 The only move 24.fxe5 Nd7 25.Re1 f4 26.Nd5! [26.Ne2 g5 27.Nd4 Nxe5 28.Nxe6 (28.Rxe6 Rae8±) 28...Rg8±] 26...f3!? [The alternatives do not leave Black any chances: 26...g5 27.Nc7 Nxe5 28.Rxe6 (28.Nxa8 Rxa8±) 28...Rae8 29.Rh6+-; 26...Nxe5 27.Nxf4 Bd7 28.c5! Rad8 (28...Ke7 29.Nd5+!+-) 29.Nd3+-] 27.Nc7 [27.gxf3?! Nxe5 28.Kg2 Rfd8 29.Rxd8 Rxd8 30.Kg3 g5 is just marginally better for the first player; 27.Rd1!+-] 27...Nxe5 28.Rxe6?! [28.Red1!+-; 28.Nxa8? f2+! 29.Kxf2 Ke7+ 30.Ke3 Kxd6 31.Rd1+ Kc5 32.Nc7 Rf6 33.Rd8 Bd7 is only slightly better for White] 28...Rad8!!

The best practical chance! In return for the sacrificed piece I limit all the white pieces, deprive the white king of pawn cover, get control over the second rank, and will have a strong passed pawn on f3. [28...Rae8!? 29.Rxe8 Bxe8 30.Rd1 fxg2 31.Kxg2 Ke7±; 28...Nd7? 29.Rf1! (29.Rxc6! Rac8 30.Rd1!+-; 29.Rd1!+-) ] 29.Rxe5 Rd2 30.Rc1 [Deserved attention: 30.gxf3!? Rxc2 31.Rd1 Rxa2 32.Ne6 Re8 33.Rd6± However, for a human being it is too difficult to leave the control over the second rank for a mere pawn.] 30...Rxg2+ 31.Kh1 Only move as: [31.Kf1? Bd7!–+] 31...Kf6!

There is noone else left on the board, and His Majesty rushes in for the g3 square, to attack. This is an idea without which 28...Tad8!! would not be possible.32.Re6+! [32.Ra5?! Rd2!! (During the game I was counting on the move: 32...b6! but after the subtle: 33.Rf1! Black can hardly save himself. The other continuations are not dangerous, for example: a) 33.Nd5+ Kg5 34.Nxb6+ (34.Rxa6 Kh4=) 34...Kh4 35.Bd3 Rd2 36.Bf1 Rf4 (36...Bxe4 37.Re5 Bf5 with an attack) 37.b4 Rxe4 38.Nd5 Kg3 39.Ra3 Bxd5 40.cxd5 Rxb4 41.Kg1 Rbb2 42.Rcc3 Rf2 43.Rc1 Rbd2 and only Black can play for a win; b) 33.Ra3 Rd2! 34.Bb1 Ke5! 35.Nd5 Bd7 with a clear edge; c) 33.Rxa6 Kg5! 34.Ne6+ Kh4 35.Nxf8 (35.Ra7 Kg3 36.Rg1 Kf2=) 35...Kg3 36.Rg1 Kf2=; 33...Rxc2 34.Rxf3+ Kg7 35.Ne6+ (35.Rxf8 Kxf8 36.Rxa6 Bxe4+ 37.Kg1) 35...Kh6 36.Rxf8 bxa5 37.Nc5 Re2 38.Kg1 a4 39.Rf2 Re1+ 40.Rf1 Re2 41.Rf6 Bxe4! 42.Nxe4! (42.Re6 Rxa2! 43.Rxe4 a3=) 42...Rxe4 43.Rxa6 axb3 44.axb3 Kg5!± And with correct play Black can escape, for instance: 45.c5 Re3 46.b4 Rb3 47.Rb6 Kf4 48.Rb7 Kf3 +/=) 33.Bb1 b6! (33...Rf7!?) 34.Nd5+ a) 34.Rxa6 Ke5! with devastating attack, here is a sample line: (34...Bd7!?) 35.Nd5 Bd7 36.Nxb6 Bxh3 37.Ra5+ Kf4 38.Rd5 Rxd5 39.cxd5 Kg3 40.Rc3 Bg2+ 41.Kg1 Rf4–+; b) 34.Ra3 Ke5-/+; 34...Kg5 35.Rxa6 (35.Nxb6+ Kh4-/+) 35...Bd7!? (35...f2 36.Rf1 Bd7 37.Kh2 Kh4 38.Ra7 Rf3=) 36.Ra7 Bxh3 and the attack is too strong.; 32.Rc5? Ke7 33.Nd5+ Kd6 34.Ra5 Rxc2 35.Rxc2 f2 36.Rc1 f1Q+ 37.Rxf1 Rxf1+ 38.Kg2 Re1=] 32...Kg5 33.Rg1! [The other moves lead to a draw: 33.Rxc6? bxc6 34.Ne6+ Kh4 35.Nxf8 Kg3 36.Rg1 Kf2=; 33.Re7? Kh4 34.Rg1 Kg3 35.Rxh7 Kf2=; 33.Bd3?! Kf4 34.Bf1 Rxa2 with unclear play] 33...Rxg1+!? [After: 33...Rf7 34.Rxg2+ fxg2+ 35.Kxg2 Rxc7 36.Kg3 Rd7 37.h4+ Kh6 38.Rf6± Black's position remains difficult. The move in the text is the best chance for Black.] 34.Kxg1 f2+ 35.Kf1 Bd7! 36.e5? This move lets the win slip away. [Hardly better was: 36.Bd1? Rf7! 37.Bg4 h5 38.Re5+ Kf4 39.Be6! Re7!=; The win is simple, and surprising: 36.Re5+!

36...Kh4 37.Ne6 Re8 38.Kxf2 Rxe6 39.Rxe6 Bxe6 40.e5! Bxh3 41.Be4 b6 42.b4 h5 43.c5 bxc5 44.bxc5 Bc8 45.c6 Kg4 46.Ke3+-] 36...Kh4! 37.Be4 [37.Rf6? Rxf6 38.exf6 Kg3–+] 37...Kg3 38.Bxb7?? But this move loses. [The only move was: 38.Bg2 Rf4 39.Rd6 Bf5! 40.Ne6 again the only move as (40.e6? Rf3!–+) 40...Rf3! 41.Nc5! Re3 42.Rd1! Bc2 43.e6 b6 44.Ne4+ Bxe4 45.Bxe4 Rxe4 46.Rd3+ Kh4= with a draw.] 38...Rf4–+

39.Bd5 [39.Bg2 Rd4 40.Rd6 Rxd6 41.exd6 Bf5–+] 39...Rd4 [39...Rf5!–+] 40.Rf6 [40.Ke2 Rf4 (40...Bxe6 41.Nxe6 Rxd5 42.cxd5 Kg2 43.Nf4+ Kg1–+) 41.Kf1 Rf5–+] 40...Rd1+ 41.Ke2 Re1+ 42.Kd2 Bf5 0–1
Naiditsch,Arkadji (2674) - Nikolov,Momchil (2549) [B42]
EU Plovdiv 2010 (4), 20.10.2010
[Momchil Nikolov]
1.e4 c5 2.Nf3 e6 3.d4 cxd4 4.Nxd4 a6 5.Bd3 Nf6 6.0–0 Qc7 7.Qe2 d6 8.c4 g6 9.Nc3 Bg7 10.Nf3 0–0 11.Rd1 Nc6 12.Bc2 Ng4 13.Ne1?!

13...f5?! [13...Nge5! 14.f4 Nd7 15.Nf3 Na5! 16.Bd3 Nb6! (16...b6=) 17.c5! dxc5 18.Be3 Nd7! 19.Rac1 c4 20.Bb1 b5 with good play] 14.h3 Nf6?! [14...Nge5 15.f4 Nf7 16.Nf3 Bd7=] 15.Nf3 Ne5 [15...fxe4 16.Nxe4 Nxe4 17.Bxe4 Ne5 is better for White] 16.Nxe5 dxe5 17.b3! Rf7 18.Ba3 Bf8 [18...Qa5 19.Na4 Bd7 20.b4 Qc7 21.Nc5±] 19.Bxf8 Rxf8 20.Qd2 Bd7 21.Qd6 Qxd6? [21...Rac8! 22.Rd3 a) 22.f4 exf4 23.e5 Nd5! This was the move that I missed while calculating the option: (21...Tac8!)- 24.Nxd5 (24.Qxc7 Rxc7 25.Nxd5 exd5 26.Rxd5 Re8) 24...exd5 25.Qxd5+ Rf7= 26.e6 Qb6+; b) 22.Rd2 b5!; 22...b5! 23.exf5 Qxd6 24.Rxd6 gxf5 25.Rxa6 bxc4 26.b4 Ra8=] 22.Rxd6 Kf7?! [22...Rad8? 23.Rad1 f4 (23...Kf7 24.f4!+-) 24.Na4+-; 22...Rae8!? 23.f4 Bc8! 24.fxe5 Nd7 25.Na4 Nxe5 26.Nb6±] 23.f4! Bc6 The only move 24.fxe5 Nd7 25.Re1 f4 26.Nd5! [26.Ne2 g5 27.Nd4 Nxe5 28.Nxe6 (28.Rxe6 Rae8±) 28...Rg8±] 26...f3!? [The alternatives do not leave Black any chances: 26...g5 27.Nc7 Nxe5 28.Rxe6 (28.Nxa8 Rxa8±) 28...Rae8 29.Rh6+-; 26...Nxe5 27.Nxf4 Bd7 28.c5! Rad8 (28...Ke7 29.Nd5+!+-) 29.Nd3+-] 27.Nc7 [27.gxf3?! Nxe5 28.Kg2 Rfd8 29.Rxd8 Rxd8 30.Kg3 g5 is just marginally better for the first player; 27.Rd1!+-] 27...Nxe5 28.Rxe6?! [28.Red1!+-; 28.Nxa8? f2+! 29.Kxf2 Ke7+ 30.Ke3 Kxd6 31.Rd1+ Kc5 32.Nc7 Rf6 33.Rd8 Bd7 is only slightly better for White] 28...Rad8!!

The best practical chance! In return for the sacrificed piece I limit all the white pieces, deprive the white king of pawn cover, get control over the second rank, and will have a strong passed pawn on f3. [28...Rae8!? 29.Rxe8 Bxe8 30.Rd1 fxg2 31.Kxg2 Ke7±; 28...Nd7? 29.Rf1! (29.Rxc6! Rac8 30.Rd1!+-; 29.Rd1!+-) ] 29.Rxe5 Rd2 30.Rc1 [Deserved attention: 30.gxf3!? Rxc2 31.Rd1 Rxa2 32.Ne6 Re8 33.Rd6± However, for a human being it is too difficult to leave the control over the second rank for a mere pawn.] 30...Rxg2+ 31.Kh1 Only move as: [31.Kf1? Bd7!–+] 31...Kf6!

There is noone else left on the board, and His Majesty rushes in for the g3 square, to attack. This is an idea without which 28...Tad8!! would not be possible.32.Re6+! [32.Ra5?! Rd2!! (During the game I was counting on the move: 32...b6! but after the subtle: 33.Rf1! Black can hardly save himself. The other continuations are not dangerous, for example: a) 33.Nd5+ Kg5 34.Nxb6+ (34.Rxa6 Kh4=) 34...Kh4 35.Bd3 Rd2 36.Bf1 Rf4 (36...Bxe4 37.Re5 Bf5 with an attack) 37.b4 Rxe4 38.Nd5 Kg3 39.Ra3 Bxd5 40.cxd5 Rxb4 41.Kg1 Rbb2 42.Rcc3 Rf2 43.Rc1 Rbd2 and only Black can play for a win; b) 33.Ra3 Rd2! 34.Bb1 Ke5! 35.Nd5 Bd7 with a clear edge; c) 33.Rxa6 Kg5! 34.Ne6+ Kh4 35.Nxf8 (35.Ra7 Kg3 36.Rg1 Kf2=) 35...Kg3 36.Rg1 Kf2=; 33...Rxc2 34.Rxf3+ Kg7 35.Ne6+ (35.Rxf8 Kxf8 36.Rxa6 Bxe4+ 37.Kg1) 35...Kh6 36.Rxf8 bxa5 37.Nc5 Re2 38.Kg1 a4 39.Rf2 Re1+ 40.Rf1 Re2 41.Rf6 Bxe4! 42.Nxe4! (42.Re6 Rxa2! 43.Rxe4 a3=) 42...Rxe4 43.Rxa6 axb3 44.axb3 Kg5!± And with correct play Black can escape, for instance: 45.c5 Re3 46.b4 Rb3 47.Rb6 Kf4 48.Rb7 Kf3 +/=) 33.Bb1 b6! (33...Rf7!?) 34.Nd5+ a) 34.Rxa6 Ke5! with devastating attack, here is a sample line: (34...Bd7!?) 35.Nd5 Bd7 36.Nxb6 Bxh3 37.Ra5+ Kf4 38.Rd5 Rxd5 39.cxd5 Kg3 40.Rc3 Bg2+ 41.Kg1 Rf4–+; b) 34.Ra3 Ke5-/+; 34...Kg5 35.Rxa6 (35.Nxb6+ Kh4-/+) 35...Bd7!? (35...f2 36.Rf1 Bd7 37.Kh2 Kh4 38.Ra7 Rf3=) 36.Ra7 Bxh3 and the attack is too strong.; 32.Rc5? Ke7 33.Nd5+ Kd6 34.Ra5 Rxc2 35.Rxc2 f2 36.Rc1 f1Q+ 37.Rxf1 Rxf1+ 38.Kg2 Re1=] 32...Kg5 33.Rg1! [The other moves lead to a draw: 33.Rxc6? bxc6 34.Ne6+ Kh4 35.Nxf8 Kg3 36.Rg1 Kf2=; 33.Re7? Kh4 34.Rg1 Kg3 35.Rxh7 Kf2=; 33.Bd3?! Kf4 34.Bf1 Rxa2 with unclear play] 33...Rxg1+!? [After: 33...Rf7 34.Rxg2+ fxg2+ 35.Kxg2 Rxc7 36.Kg3 Rd7 37.h4+ Kh6 38.Rf6± Black's position remains difficult. The move in the text is the best chance for Black.] 34.Kxg1 f2+ 35.Kf1 Bd7! 36.e5? This move lets the win slip away. [Hardly better was: 36.Bd1? Rf7! 37.Bg4 h5 38.Re5+ Kf4 39.Be6! Re7!=; The win is simple, and surprising: 36.Re5+!

36...Kh4 37.Ne6 Re8 38.Kxf2 Rxe6 39.Rxe6 Bxe6 40.e5! Bxh3 41.Be4 b6 42.b4 h5 43.c5 bxc5 44.bxc5 Bc8 45.c6 Kg4 46.Ke3+-] 36...Kh4! 37.Be4 [37.Rf6? Rxf6 38.exf6 Kg3–+] 37...Kg3 38.Bxb7?? But this move loses. [The only move was: 38.Bg2 Rf4 39.Rd6 Bf5! 40.Ne6 again the only move as (40.e6? Rf3!–+) 40...Rf3! 41.Nc5! Re3 42.Rd1! Bc2 43.e6 b6 44.Ne4+ Bxe4 45.Bxe4 Rxe4 46.Rd3+ Kh4= with a draw.] 38...Rf4–+

39.Bd5 [39.Bg2 Rd4 40.Rd6 Rxd6 41.exd6 Bf5–+] 39...Rd4 [39...Rf5!–+] 40.Rf6 [40.Ke2 Rf4 (40...Bxe6 41.Nxe6 Rxd5 42.cxd5 Kg2 43.Nf4+ Kg1–+) 41.Kf1 Rf5–+] 40...Rd1+ 41.Ke2 Re1+ 42.Kd2 Bf5 0–1
18.11.10
Free Chess Analyses from an International Master Released!
Bulgarian International Master Kalin Karakehajov had recently published a big part his analyses online. The analyses are very deep and beautiful. I am publishing probably the sharpest and most intriguing of them:
Two knights 4.Ng5 - For white [C57]
[Kalin Karakehayov]
1.e4 e5 2.Nf3 Nc6 3.Bc4 Nf6 4.Ng5 d5 5.exd5 b5

[5...Nxd5?! 6.d4! Bb4+! a) 6...Nxd4 7.c3! f6 (7...h6 8.Nxf7 Kxf7 9.cxd4; 7...b5 8.Bxd5 Qxd5 9.f3) 8.Ne4! Bf5 (8...Bg4 9.f3 Ne3 10.Bxe3 Nxf3+ 11.Kf2 Qxd1 12.Rxd1 Ng5 13.Nxg5 Bxd1 14.Nf7; 8...b5 9.Bxd5 Qxd5 10.f3 f5 11.Ng3; 8...Nb6 9.cxd4 Nxc4 10.Qa4+) 9.f3 Bxe4! (9...b5 10.Bxd5 Qxd5 11.cxd4; 9...Nb6 10.cxd4 Nxc4 11.Qa4+) 10.fxe4 Nb6 11.cxd4 Bb4+! 12.Ke2!! (12.Nc3 Qxd4 13.Be2 Qxe4 14.0–0 Qd4+ 15.Qxd4 exd4 16.Nb5 0–0–0 17.Bf4 Nd5І) 12...Nxc4 13.Qa4+ c6 (13...Qd7 14.Qxb4 Qg4+ 15.Kf2 Qh4+ (15...Nd6 16.Nc3) 16.Kf3 Qh5+ (16...Nd6 17.Nc3) 17.Kg3 Nd6 (17...Qg6+ 18.Kf2) 18.Nc3) 14.Qxb4 Qxd4 15.Nc3 b5! (15...Nd6 16.Qxd4 exd4 17.Rd1! c5 18.Bf4!) 16.Rd1 a5 17.Qb3 a4 (17...Qc5 18.a4 b4 19.Nb1 Rd8 (19...Ke7 20.Na3! Nxa3 21.Rxa3!) 20.Rxd8+ Kxd8 21.Nd2 Nd6 22.Qd3) 18.Qc2 Qc5 (18...Qb6 19.b3 axb3 20.Qxb3 0–0 (20...Qb7 21.a4 Qf7 22.Qb4!; 20...Qa6 21.Qb4!) 21.a4+-) 19.Rb1! 0–0 (19...Qb4 20.b3 axb3 21.Qxb3; 19...Ra5 20.b4 axb3 21.Qd3!; 19...b4 20.Nxa4 Qb5 21.Qd3!) 20.Nxa4! Rxa4 (20...bxa4 21.b3 axb3 22.axb3 Rfb8 23.Bd2+-) 21.b3 Ra6 22.bxc4 Rfa8 (22...Ra4 23.Be3 Qxc4+ (23...Rxc4 24.Qb3 Qe7 25.Rbc1) 24.Qxc4+ Rxc4 25.Rbc1) 23.a3 Ra4 24.Rb4! Rxb4 25.axb4 Qxb4 26.cxb5 cxb5 27.Be3+-; b) 6...Qd6 7.0–0 Be6 (7...Nxd4 8.c3) 8.Nxe6 fxe6 (8...Qxe6 9.dxe5) 9.dxe5 Nxe5 10.Bxd5 exd5 11.Bf4 0–0–0 12.Re1 Re8 13.Nc3±; c) 6...exd4 7.0–0! Be6 c1) 7...f6? 8.Re1+ Be7 (8...Ne5 9.Nf3 Be7 10.Nxe5 fxe5 11.Qh5+ Kf8 12.Rxe5 c6 13.Bxd5 cxd5 14.Qf3+ Bf6 15.Bg5) 9.Nc3!! dxc3 c11) 9...fxg5 10.Nxd5+-; c12) 9...Nxc3 10.Qh5+ g6 (10...Kd7? 11.Be6+ Kd6 12.Nf7#) 11.Bf7+ Kd7 12.Qh3+ Kd6 (12...f5 13.Ne6) 13.Ne6 Ne2+ (13...Ne5 14.bxc3; 13...Bxe6 14.Qxe6+ Kc5 15.bxc3) 14.Rxe2 Bxe6 (14...Ne5 15.Qa3+) 15.Rxe6+ Kc5 16.Qa3++-; c13) 9...Ncb4 10.Nxd5 Nxd5 11.Qh5+ g6 12.Qh6 fxg5 13.Qg7+-; 10.Bxd5 fxg5 11.Bxg5 cxb2 (11...Kf8 12.Qf3+ Bf6 13.Rad1! Nd4 (13...Bd7 14.Bc4!+-) 14.Rxd4 c6 15.Rf4) 12.Bxc6+ bxc6 (12...Kf7 13.Bd5+) 13.Qxd8+ Kxd8 14.Bxe7+ Ke8 15.Ba3+ Kf7 16.Re7+! Kf6 17.Rb1+-; c2) 7...h6 8.Nxf7 Kxf7 9.Qf3+ Qf6 10.Bxd5+±; c3) 7...Be7 8.Nxf7 Kxf7 9.Qf3+ Ke8 (9...Ke6 10.Qe4+) 10.Bxd5±; 8.Re1 Qd6 (8...Qd7 9.Nxf7 Kxf7 10.Qf3+ Kg8 11.Rxe6 Ncb4 (11...Rd8 12.Qe4!! h6 13.Bf4 Na5 14.Bxd5 Qxd5 15.Bxc7 Rd7 16.Bxa5 Qxa5 17.Re8+-) 12.Re4±) 9.Nxf7! Kxf7 10.Qf3+ Ke7™ 11.Bxd5 Ne5 12.Bg5+ Kd7 (12...Ke8 13.Qe4 Bxd5 14.Qxe5+±) 13.Bxe6+ Qxe6 14.Qe4 Re8 15.Qxd4+ Bd6 16.Nd2±; d) 6...Be7 7.Nxf7! Kxf7 8.Qf3+ Ke6 9.Nc3 Ncb4 (9...Nxd4 10.Bxd5+ Kd6 11.Qd3 c6 12.Be4±) 10.Qe4! c6 11.a3 Na6 (11...b5 12.Bb3 Qa5 13.Bd2+-; 11...Qa5 12.Bd2 Kd7 13.dxe5) 12.Nxd5 cxd5 13.Qxe5+ Kf7 (13...Kd7?? 14.Bb5#) 14.Bxd5+ Kf8 15.Bf4! Bf6 16.Qe4±; 7.c3 Be7 8.Nxf7! Kxf7 9.Qf3+ Ke6 10.Qe4!

10...Bf8! a) 10...Rf8 11.f4 h5 a1) 11...Qd7 12.fxe5 Rf5 13.Be2 g6 (13...h5? 14.Bxh5) 14.Bg4 Kf7 15.Bxf5 gxf5 16.Qf3±; a2) 11...b5 12.Bxb5 Bb7 13.fxe5+-; a3) 11...g6 12.0–0 Qd7 13.fxe5 Rf5 14.Qg4+-; 12.fxe5 Rf5 13.Bd3 Kf7 14.Qe2 g6 15.Bxf5 Bxf5 16.0–0±; b) 10...g5 11.Nd2! Rf8 (11...Bf6 12.Nf3 Rg8 13.dxe5 Nxe5 (13...Bxe5 14.Bxg5 Rxg5 15.Bxd5++-) 14.Nd4++-) 12.Nf3 Rxf3 (12...Rf5 13.g4 Rxf3 14.Qxf3 Na5 15.Qf5+ Kd6 16.Qxe5+ Kc6 17.Bd3 Bxg4 b1) 17...Bf6 18.Qe4 Qe7 (18...b5 19.b4!+-) 19.Qxe7 Bxe7 20.b4±; b2) 17...b5 18.Qe2 a6 19.Bxh7±; 18.c4 Nxc4 19.Bxc4 Bf3 20.Rg1±) 13.gxf3! b5 (13...Qd6 14.h4! Nxd4 15.hxg5+-) 14.Bxb5 Bb7 15.Bxc6 Bxc6 16.c4 Nb4 17.d5+ Nxd5 18.cxd5+ Qxd5 19.Qg4+ Kf7 20.Bxg5 Qxf3 21.Rg1 Rg8 22.Qxf3+ Bxf3 23.Rg3±; c) 10...Qd6? 11.f4 Na5 12.dxe5; d) 10...b5 11.Bxb5 Bb7 12.f4 a6 (12...Kf7 13.fxe5 a6 14.0–0+ Ke8 15.Ba4+-) 13.Bxc6 Bxc6 14.fxe5 Rf8 (14...Kf7 15.c4 Nb4 16.d5±) 15.Qg4+ Kf7 16.0–0+ Ke8 (16...Kg8? 17.Qe6+) 17.Rxf8+ Kxf8 18.Qf5+ Ke8 19.Qxh7±; 11.f4 Nce7 12.fxe5 c6 13.0–0 Kd7! (13...h5 14.Bb3 b5 15.Bg5 Kd7 16.Nd2±) 14.Be2! Ke8! (14...Kc7 15.c4 Nb4 (15...Nb6? 16.e6+-) 16.e6 b6 17.a3 Na6 18.Bf4+ Kb7 19.Rd1 Qe8 20.d5 Nc5 21.Qe5 Ng6 22.Qc7+ Ka6 23.Bd2!+-) 15.c4 Nb6!N a) 15...Nb4 16.a3 Na6 17.Nc3 Be6 18.Bg5±; b) 15...Nc7 16.Be3! g6 (16...Be6 17.Nc3 Qd7 18.Rad1±) 17.Nc3 Bf5 18.Qh4; 16.Be3 Be6 17.b3© In case of g6, Be3-g5-f6 with a difficult position for black...; 5...Nb4?! 6.d6! Nbd5 a) 6...Qxd6?! 7.Bxf7+ Ke7 8.Bb3±; b) 6...Nfd5?! 7.d4! Qxd6 b1) 7...Bf5? 8.Bxd5 Nxc2+ (8...Nxd5 9.Qf3 Be6 10.Nxe6 fxe6 11.Qh5++-) 9.Kf1 Qxd6 (9...Nxa1 10.Nxf7 Qd7 11.Nc3+-) 10.Nc3 Nxa1 11.Nxf7 Qa6+ 12.Kg1+-; b2) 7...h6 8.Nxf7 Kxf7 9.a3±; b3) 7...Bxd6? 8.a3+-; 8.c3 Nc6 b1) 8...h6 9.Nf3 e4 10.Ne5 Nc6 11.Nxc6 bxc6 (11...Qxc6? 12.Qb3+-) 12.0–0±; b2) 8...f6 9.Ne4 Qc6 10.Na3 Nxc3 (10...Bd7 11.cxb4 Bxb4+ 12.Nd2 Nf4 (12...Bxa3 13.Qb3! Nf4 14.d5±) 13.d5) 11.Nxc3 Qxg2 12.Rf1±; 9.0–0! Be6™ 10.dxe5 Nxe5 (10...Qd7 11.Nxe6 fxe6 12.Qe2±) 11.Nxe6 fxe6 (11...Nxc4 12.Qxd5! Qxe6 13.Qxb7+-) 12.Bxd5 exd5 13.Bf4 0–0–0 14.Qh5 g5™ 15.Bxg5! Be7 16.Bf4! Bf6 17.Nd2 Rde8 18.Rfe1! Bg7! 19.Rad1 Qg6 20.Qxg6 Nxg6 21.Be3±; 7.dxc7 Qxc7 8.d3 Bc5 a) 8...h6?! 9.Ne4 Bg4 (9...Nxe4 10.Bb5+ Bd7 11.Bxd7+ Qxd7 12.dxe4±) 10.f3 Bd7 11.0–0±; b) 8...Bg4 9.f3 Bd7 10.Ne4 Be7 (10...b5 11.Bb3 Be7 12.Nxf6+ Nxf6 13.Nc3±) 11.Nxf6+ Nxf6 12.Nc3 0–0 13.Qe2 Bc5 14.Be3±; c) 8...Bd6!? 9.Ne4 Nxe4 (9...0–0 10.Nxd6 Qxd6 11.0–0±) 10.Bb5+ Ke7! (10...Bd7 11.Bxd7+ Qxd7 12.dxe4 Nf6 13.Nc3 Bb4 14.Qxd7+ Kxd7 15.Bd2±) 11.dxe4 Qa5+ 12.Qd2 Qxb5 (12...Qxd2+ 13.Bxd2!± Nf4 (13...Nb4 14.Bxb4 Bxb4+ 15.c3 Bc5 16.Bc4±) 14.Bf1!±) 13.exd5І; 9.Ne4 Nxe4 (9...0–0 10.Nbc3±; 9...Bg4 10.Nxf6+ Nxf6 11.f3 Bd7 12.Nc3±) 10.dxe4 Nf6! a) 10...Nf4 11.Bxf4 exf4 12.Bb5+±; b) 10...Nb6 11.Bb5+ Bd7 (11...Ke7 12.0–0±) 12.Bxd7+±; c) 10...Bb4+ 11.c3 Qxc4 12.Qxd5 Qxd5 13.exd5 Bd6 14.Be3±; d) 10...Nb4 11.a3; 11.Bb5+ Ke7! (11...Bd7 12.Bxd7+ Qxd7 13.Qxd7+ Kxd7 14.f3±) 12.0–0! Nxe4 a) 12...Rd8 13.Qf3±; b) 12...a6 13.Bd3 Bg4 14.Qe1±; c) 12...Bg4 13.Qd3 a6 (13...Be6 14.Qf3 Rhd8 15.Bg5±) 14.Bc4 Rhd8 15.Bd5±; 13.Qf3! Nd6! a) 13...Nf6 14.Bg5±; b) 13...f5!? 14.Bd3 Qc6! b1) 14...Nd6 15.Qg3 Kf6 16.Nc3 Be6 17.Re1 Bd4 18.Ne2 Bc5 (18...Bb6 19.Nf4!+-) 19.b4 Bb6 20.Nf4!+-; b2) 14...Rf8 15.Bxe4 fxe4 16.Bg5+ Ke8 17.Qxe4 Bf5 18.Qe2±; b3) 14...Nxf2 15.Rxf2 e4 (15...Qb6 16.Nc3 Bxf2+ 17.Qxf2 Qxf2+ 18.Kxf2 h6 19.Be3 Be6 20.g4! g6 21.Re1! b6 22.Bf4! e4™ 23.Ba6±) 16.Bg5+ Ke8 17.Bb5+ Bd7 b31) 17...Kf8 18.Qe2 Qb6 (18...a6 19.Ba4 Qb6 20.Bb3 Bd7 21.Nc3 Bxf2+ 22.Qxf2 Qxf2+ 23.Kxf2±) 19.Nc3 Bxf2+ (19...a6 20.Nxe4!+-) 20.Qxf2 Qxf2+ 21.Kxf2±; b32) 17...Kf7 18.Qh5+ g6 19.Qe2±; 18.Qxf5 Bxf2+

19.Kf1!! Bxb5+ 20.Qxb5+±; 15.Be3 Bd6 16.Bxe4 Qxe4 17.Qxe4 fxe4 18.Nc3 Bf5 19.Rad1І; 14.Nc3 Be6 15.Bd3І; 5...Nd4 6.c3 b5 (6...Nf5 7.0–0 h6 (7...Nxd5 8.Re1І; 7...Bd6 8.d4І) 8.Nf3 e4 9.Ne5 Bd6 10.d4 0–0 (10...exd3 11.Nxd3 0–0 12.Bf4І) 11.f3І) 7.Bf1 is covered below] 6.Bf1! Nd4 [6...h6 7.Nxf7 Kxf7 8.dxc6 Bc5 a) 8...Qd6 9.Bxb5 Qd5 10.Bf1 Bc5 11.Nc3 Qxc6 12.Bc4+±; b) 8...Qd5 9.Qf3 Qc5 (9...e4 10.Qb3; 9...Qxf3 10.gxf3 a6 11.Nc3±) 10.Nc3 Bg4 (10...b4 11.Ne4 Qd4 (11...Qxc2 12.Bd3; 11...Qd5 12.Bd3) 12.Nxf6 gxf6 13.Be2+-) 11.Qe3 a6 (11...Qxc6 12.f3 Bc5 13.Bxb5 Qd6 14.Ne4 Nxe4 15.Qxe4 Be6 16.Bc4+-) 12.Qxc5 Bxc5 13.Be2±; 9.Be2 Ne4 a) 9...e4 10.0–0±; b) 9...Qd5 10.0–0 Qxc6 11.d3 Rd8 (11...Bb7 12.Bf3 e4 13.dxe4 Rad8 14.Qe2±) 12.Nc3±; 10.0–0 Bxf2+ a) 10...Qf6 11.Qe1; b) 10...Rf8 11.Nc3 Nxf2 (11...Nxc3 12.dxc3; 11...Bxf2+ 12.Kh1+-) 12.Ne4 Kg8 13.Nxf2 Qf6 14.d4 Bxd4 15.Kh1 Bxf2 16.Be3 Rd8 (16...Qh4 17.Qd5+ Kh8 (17...Kh7 18.Bd3+) 18.Qc5) 17.Qb1 Bxe3 18.Rxf6 gxf6 19.Qe1+-; c) 10...Nxf2 11.d4 Bxd4 12.Rxf2+ Bxf2+ 13.Kxf2+-; d) 10...Qh4 11.Qe1; 11.Rxf2+ Nxf2 12.Qf1! Rf8 13.Qxf2+ Kg8 14.Qe3 Qh4 15.Bf3 Bg4 (15...Qf6 16.Qe2+-) 16.Bd5+ Kh8 17.d3 Be2 (17...Rad8 18.Be4+-) 18.Qxe2 Qd4+ 19.Kh1 Qxd5 (19...Rf2 20.Qe1 Raf8 21.Bf3+-) 20.Nc3 Qxc6 21.Be3+-; 6...Nxd5?! 7.Bxb5 Bb7 8.d4!±; 6...Bg4?! 7.f3 Nxd5 8.Nxf7 Kxf7 9.fxg4 Nf4 10.Nc3±; 6...Qxd5?! 7.Nc3±] 7.c3 Nxd5 [7...Nf5?! 8.Bxb5+ Bd7 9.Qe2] 8.cxd4 Qxg5 9.Bxb5+ Kd8 [9...Bd7 10.Bxd7+ Kxd7 11.0–0 Nf4 (11...Bd6 12.d3; 11...exd4 12.d3 Qf6 13.Qg4+ Kc6 14.Nd2±) 12.g3 Qg6!? a) 12...Nd3 13.Qf3; b) 12...Nh3+ 13.Kg2 Nf4+ 14.Kh1 Nd3? 15.Qf3+-; c) 12...exd4 13.d3 Bd6 (13...Nh3+ 14.Kg2 Qf5 15.Qa4+ Kc8 (15...Ke7 16.Qc6) 16.Qe8+ Kb7 17.Qe4+ Qxe4+ 18.dxe4+-) 14.Bxf4 Bxf4 15.Qa4+±; 13.d3!? Nxd3 14.dxe5 Bc5 15.Nc3 Kc8 (15...Rhd8 16.Bg5!) 16.Qe2 Re8 17.Be3 Bxe3 (17...Rxe5? 18.Rad1 Bxe3 19.fxe3 Nc5 20.Qc4+-) 18.fxe3!± The knight can't hold d3 and white is much better] 10.0–0 Bb7 [10...Nf4 11.Bc6! Rb8 a) 11...e4 12.Bxe4 Bg4 13.Bf3 h5 (13...Bxf3 14.Qxf3 Rb8 15.d3 Bd6 16.Nc3±) 14.d3 Bd6 15.Nc3±; b) 11...Bg4 12.Bf3 Bxf3 b1) 12...f5? 13.dxe5 Nxg2 14.d4 Nf4 15.Bxg4 fxg4 16.Qb3 Rc8 17.Qe3 Nh3+ 18.Qxh3 Qxc1 19.Rxc1 gxh3 20.Nc3+-; b2) 12...h5 13.dxe5 Qxe5 14.d4 Qf5 15.Nd2 Bd6 16.Re1 (16.h3? Nxh3+ 17.gxh3 Qf4ч) 16...Nd3 17.Re2 Nf4 18.Re4±; 13.Qxf3 Rb8 14.dxe5 Qxe5 15.Nc3 Bd6 16.g3 Ne6 17.d3±; 12.dxe5 Nd3!? (12...Bg4 13.Bf3 Bxf3 14.Qxf3 Qxe5 15.Nc3 Bd6 16.g3!±; 12...Bd7 13.Be4 Qxe5 14.Nc3 Bd6 15.g3!±; 12...Rb6 13.Be4 Qxe5 14.Nc3 Bd6 15.g3) 13.Be4! Ba6

(13...Nxc1 14.d4 Rxb2 15.Qxc1 Qxc1 16.Rxc1±; 13...Bh3? 14.Qc2 Nf4 15.d4; 13...Bg4 14.Qc2 Nxc1 15.Rxc1 Qxe5 16.d4) 14.Re1!! Nxe1 a) 14...Qf4 15.Bxd3 Bxd3 16.Re3 Qf5 17.Nc3 Bc5 18.Rf3 Qg6 (18...Qd7 19.Qa4+-) 19.Rg3 Qf5 20.Qf3+-; b) 14...Bc5? 15.Bxd3 Bxd3 16.Qf3+-; 15.d4 Qh4 16.Qxe1± Rb4?! 17.Nc3 Rxd4? 18.Be3+-; 10...exd4!? 11.Bc6 Rb8 12.d3 Nf4 (12...Qf5!? 13.Re1 Bd6 14.Nd2 Rb6 15.Bxd5 Qxd5 16.Nc4І) 13.Na3! Bxa3 a) 13...Rb6 14.Qf3 Qf6 (14...Nh3+ 15.Qxh3 Qc5 16.Qh4+ Be7 17.Qe4 Rxc6 18.b4 f5 19.Qf3 Qb6 20.Nc4 Rxc4 21.dxc4±; 14...Qg6 15.Qxf4 Rxc6 16.Nc4; 14...Bd6 15.Nc4!) 15.Bxf4 Qxc6 (15...Rxc6 16.Qd5++-) 16.Qg3±; b) 13...Nh3+ 14.Kh1 Qf6 15.Qf3 Rb6 16.Qd5+ Qd6 17.Ba8; c) 13...Bg4 14.Qc2 Bd6 15.Re1; 14.bxa3 Bg4 15.Qc2‚; 10...Rb8 11.Bc6 exd4 (11...Nb4 12.d3 Qg4 13.Bf3 Qxd4 14.Nc3±; 11...Nf4 12.dxe5 is already covered) 12.d3 is already covered; 10...Bg4 11.Be2 Bxe2 12.Qxe2 exd4 13.d3 Qf5 14.Nd2±] 11.Qf3 Rb8 [11...exd4!? 12.d3 Qe5 a) 12...Qf6 13.Qg4! Bc8 14.Qh5 Qf5 (14...Qe6 15.Qh4+ Be7 16.Qxd4 Bf6 17.Qc5; 14...Nf4 15.Bxf4 Qxf4 16.Qd5+ Bd6 17.g3 Qf5 18.Qxa8 Qxb5 19.Na3±; 14...Ne7 15.Bc4!) 15.Qh4+ Be7 16.Qxd4 Bf6 17.Qe4 Rb8 18.Na3; b) 12...Nf4 13.Bxf4 Qxb5 14.Qg3 Qd7 b1) 14...Qb6 15.Nd2; b2) 14...c5 15.Na3 Qc6 16.Rfe1! Qg6 (16...h5 17.Bd2 Qc7 18.Qg5+ f6 19.Qg6) 17.Bg5+ f6 (17...Kd7 18.Nb5 Rc8 19.Nxa7 Ra8 20.Nb5 Rc8 21.a4±) 18.Nb5 Rc8 19.Nd6 Rc7 (19...fxg5 20.Nxb7+ Kd7 21.b4+-) 20.Nxb7+ Rxb7 21.Qf3 Qf7 22.Bd2+-; b3) 14...Rc8 15.Nd2 f6 16.Rac1 Qd7 17.Ne4±; 15.Nd2 f6 16.Rac1 Rc8 17.Ne4±; c) 12...Qg6 13.Bc4 Qc6 (13...c6 14.Nd2) 14.Nd2; 13.Nd2 Bd6 (13...a6 14.Nc4 Qf6 (14...Qe6 15.Ba4 Rb8 (15...Be7 16.Na5±) 16.Bg5+ f6 17.Rfe1 Ne3 18.Qg3 fxg5 (18...Bb4 19.Bf4) 19.fxe3±) 15.Qg4! Qe6 (15...Bc8 16.Qh5 Qe6™ 17.Ne5 g6 (17...Nf6 18.Nxf7+ Ke7 19.Qf3) 18.Qh4+ Be7 19.Nc6+ Kd7 20.Nxe7+ axb5 21.Qxd4 Bb7 22.Bg5!±) 16.Bg5+ Be7 17.Bxe7+ Nxe7 (17...Qxe7? 18.Na5+-) 18.Qxd4+ Qd5 19.Qxd5+ Nxd5 20.Ba4 Nf4 21.Ne5±) 14.g3 Qf6 a) 14...Be7 15.Nb3! Rb8 16.Na5!; b) 14...a6 15.Nc4 Qf6 (15...Qe6 16.Na5 axb5 17.Nxb7+ Kd7 18.Nxd6±) 16.Qg4! Bc8 17.Qh5 Ne7 (17...Qe6 18.Bc6 Nf6 19.Bg5 Be7 20.Bxf6 Qxc6 21.Bxg7+-) 18.Bg5 Qg6 19.Bxe7+ Kxe7 (19...Bxe7? 20.Qd5+) 20.Qh4+ Qf6 21.Qe4+ Be6 22.Nxd6 axb5 (22...Kxd6 23.Qc6+ Ke7 24.Qc5+! Kd8 25.Rac1+-) 23.Nxb5+-; c) 14...Nb6 15.Qxb7 Qxb5 16.Qf3±; d) 14...Rb8 15.Nc4 Qf6 d1) 15...Nb4 16.Nxe5 Bxf3 17.Nxf7+ Ke7 18.Bc4±; d2) 15...Qe6 16.Na5! Be7 (16...Ba8 17.Bc6±) 17.Nxb7+ Rxb7 18.Bc4 c6 19.Bd2±; d3) 15...Nc3 16.Nxe5 Bxf3 17.Nxf7+ Ke7 18.bxc3 Kxf7 19.Bc4+ Kf6 20.cxd4±; 16.Qxf6+ Nxf6 17.Nxd6 cxd6 18.Bf4І Bd5 19.a4 Nd7 20.Bxd6 Rb6 21.Bf4 a6 22.Bxd7 Kxd7 23.Be5; 15.Qg4 Nb6! a) 15...Bc8 16.Qe4 Bb7 (16...Nb6 17.Nf3) 17.Nf3 h6 18.Nxd4 Bc5 19.Qf5 Qxf5 20.Nxf5±; b) 15...c6 16.Ne4 h5™ 17.Qd1 Qg6 b1) 17...Qe6 18.Bc4 Be7 19.Re1 Qf5 (19...h4 20.Nc5 Qc8 21.Nxb7+ Qxb7 22.g4 Qd7 23.Qf3±) 20.Qb3 Bc8 (20...Rb8 21.Qa4) 21.Qa4 Nb6?! 22.Qxc6 Bd7 23.Nd6+-; b2) 17...Qe7 18.Bc4; b3) 17...Qe5 18.Bc4 Be7 19.Re1±; 18.Bg5+ Be7 19.Bxe7+ Nxe7 20.Bc4±; c) 15...Qe6 16.Qxg7 Be5 17.Qg5+ f6 (17...Bf6 18.Qh6±) 18.Qh4! Nf4 19.Ne4 Ne2+ 20.Kg2 Nxc1 21.Raxc1 Rb8 22.Bc4 Qf5 (22...Qe7 23.Kg1) 23.b3±; 16.Ne4 h5! a) 16...Qe5 17.Bg5+ Be7 (17...f6 18.Bf4 Qxb5 19.Qxg7 Re8 20.Nxd6 cxd6 21.Qxf6++-) 18.Bxe7+ Kxe7 (18...Qxe7? 19.Qxg7) 19.Rfc1!! (19.Rac1 Bxe4 20.Qxe4 Qxe4 21.dxe4 a6 22.Rxc7+ Kd8 23.Rb7 axb5 24.Rxb6 Re8І) 19...Bxe4 (19...Kf8 20.Bc6±; 19...h5 20.Qh4+ f6 21.Bc6 Bxc6 22.Rxc6 g5 23.Qh3±) 20.Qxe4 Qxe4 21.dxe4±; b) 16...Qg6 17.Qxg6 hxg6 18.Bg5+ Be7 (18...Kc8 19.Nxd6+ cxd6 20.Rac1+ Kb8 21.Bf4+-; 18...f6 19.Nxf6±) 19.Bxe7+ Kxe7 20.Rac1 Rhc8 b1) 20...Bxe4 21.Rfe1!±; b2) 20...Rac8 21.Rfe1 Kd8 (21...Kf8? 22.Nd6+-) 22.Ng5 Bd5 23.Bc6 Rf8 24.a3 Bxc6 25.Rxc6 Kd7 26.Rec1+-; b3) 20...Kd8 21.Ng5 Rf8 22.Bc4±; 21.Rfe1 Kf8 22.Bc6 Bxc6 23.Rxc6±; 17.Qg5 Qxg5 18.Bxg5+ f6! (18...Be7 19.Bxe7+ Kxe7 20.Rac1 Kd8 (20...Rhc8 21.Rfe1 Kf8 22.b3±) 21.Ng5 Rf8 (21...Bd5 22.Bc6+-) 22.Bc4±) 19.Nxf6 c6 (19...Be7 20.Ne4) 20.Nd5+ Kd7 21.Nxb6+ axb6 22.Bc4І; 11...Bd6 12.d3; 11...a6 12.Bc4 e4 (12...exd4 13.Re1!) 13.Qxe4 Bd6 14.Nc3 Re8 15.Qf3 Qf4 (15...Qh4 16.g3) 16.Qh3 Qxd4 (16...Nf6 17.d3 Qxd4 18.Bxf7 Re7 19.Bc4 h6 20.Nd1! Qg4 21.Qxg4 Nxg4 22.Ne3±) 17.Bxd5 Bxd5 18.Nxd5 Qxd5 19.Qxh7 Kd7 20.Qh3+ f5 21.Qc3±; 11...e4 12.Qxe4 Bd6 13.Re1 c6 (13...Qe7 14.d3) 14.Bf1 Kd7 (14...f5 15.Qc2±; 14...Bc8 15.Qc2±) 15.Qf3±] 12.dxe5 Nb4 [12...Nf4 13.Qg3 Qxe5 (13...Qxg3 14.hxg3 Ne6 15.Nc3±) 14.d4 Nh3+ (14...Qxb5 15.Bxf4+-) 15.Qxh3 Qxb5 16.Nc3±; 12...Qxe5 13.d4±; 12...Ne3 13.Qh3 Qxg2+ 14.Qxg2 Nxg2 (14...Bxg2? 15.fxe3 Bxf1 16.Bxf1+-) 15.d4 Nh4 (15...Be7 16.f4 Nh4 17.Be2±; 15...f6 16.f4 Nh4 17.Be2± c5? 18.d5!) 16.Bg5+ Be7 17.Bxh4 Bxh4 18.Nc3±] 13.d4! Qg6 [13...Qxg2+ 14.Kxg2 Bxf3+ 15.Kxf3 Rxb5 16.Nc3+-; 13...Qxe5 14.dxe5 Bxf3 15.Nc3+-; 13...Bxf3? 14.Bxg5++-] 14.d5! Bxd5 15.Rd1 Rxb5 16.Nc3 Qc6 [16...Ke8 17.Nxd5 Qc6 18.e6; 16...Kc8!? 17.Nxd5 Qc6 18.Qf5+ Qe6 19.Qxe6+ fxe6 20.Nxb4 Bxb4 21.Be3±] 17.Qf5!! Be7 [17...Ke8 18.Qc8+ Ke7 19.Nxb5 Qxb5 20.Bg5+ f6 21.exf6+ Kf7 (21...gxf6 22.Qxc7++-) 22.fxg7+-; 17...Ra5 18.Bg5+ Be7 19.a3 h6 (19...f6 20.Rac1+-) 20.Rab1!

20...hxg5 (20...Na2 21.Nxd5 Rxd5 22.Qxf7+-) 21.axb4 Bxb4 22.Nxd5 Rxd5 23.Qe4+-; 17...h6 18.a3 Ra5 19.Be3 g6 (19...Qd7 20.Qb1! c6 21.axb4 Rxa1 22.Qxa1 Bxb4 23.Nxd5 cxd5 24.Qa2 Ke7 25.Rxd5+-; 19...Qe6 20.Qb1!+-; 19...Be7 20.axb4 Rxa1 21.Rxa1 Be6 22.Qd3++-) 20.Qf4 g5 21.Qxf7 Kc8 22.Qf5+ Qe6 (22...Be6 23.Qf6+-) 23.Qxe6+ Bxe6 24.axb4 Bxb4 25.Bxa7 Rxa1 26.Rxa1 Rd8 27.Be3+-; 17...g6 18.Bg5+ Be7 19.Bxe7+ Kxe7 20.Qf6+ Qxf6 21.exf6+ Kxf6 22.Nxb5+-] 18.Nxb5 Qxb5 19.a3 g6! [19...Na6 20.Qxf7 c6 21.Qxg7 Re8 (21...Rf8 22.Bg5) 22.b4!+-] 20.Qf4 Na6 [20...Nc2? 21.Qe4+-] 21.Qd4 c6 22.Qxa7±
More of this excellent stuff you can find on chessbase format here: http://online-chess.eu/
Two knights 4.Ng5 - For white [C57]
[Kalin Karakehayov]
1.e4 e5 2.Nf3 Nc6 3.Bc4 Nf6 4.Ng5 d5 5.exd5 b5

[5...Nxd5?! 6.d4! Bb4+! a) 6...Nxd4 7.c3! f6 (7...h6 8.Nxf7 Kxf7 9.cxd4; 7...b5 8.Bxd5 Qxd5 9.f3) 8.Ne4! Bf5 (8...Bg4 9.f3 Ne3 10.Bxe3 Nxf3+ 11.Kf2 Qxd1 12.Rxd1 Ng5 13.Nxg5 Bxd1 14.Nf7; 8...b5 9.Bxd5 Qxd5 10.f3 f5 11.Ng3; 8...Nb6 9.cxd4 Nxc4 10.Qa4+) 9.f3 Bxe4! (9...b5 10.Bxd5 Qxd5 11.cxd4; 9...Nb6 10.cxd4 Nxc4 11.Qa4+) 10.fxe4 Nb6 11.cxd4 Bb4+! 12.Ke2!! (12.Nc3 Qxd4 13.Be2 Qxe4 14.0–0 Qd4+ 15.Qxd4 exd4 16.Nb5 0–0–0 17.Bf4 Nd5І) 12...Nxc4 13.Qa4+ c6 (13...Qd7 14.Qxb4 Qg4+ 15.Kf2 Qh4+ (15...Nd6 16.Nc3) 16.Kf3 Qh5+ (16...Nd6 17.Nc3) 17.Kg3 Nd6 (17...Qg6+ 18.Kf2) 18.Nc3) 14.Qxb4 Qxd4 15.Nc3 b5! (15...Nd6 16.Qxd4 exd4 17.Rd1! c5 18.Bf4!) 16.Rd1 a5 17.Qb3 a4 (17...Qc5 18.a4 b4 19.Nb1 Rd8 (19...Ke7 20.Na3! Nxa3 21.Rxa3!) 20.Rxd8+ Kxd8 21.Nd2 Nd6 22.Qd3) 18.Qc2 Qc5 (18...Qb6 19.b3 axb3 20.Qxb3 0–0 (20...Qb7 21.a4 Qf7 22.Qb4!; 20...Qa6 21.Qb4!) 21.a4+-) 19.Rb1! 0–0 (19...Qb4 20.b3 axb3 21.Qxb3; 19...Ra5 20.b4 axb3 21.Qd3!; 19...b4 20.Nxa4 Qb5 21.Qd3!) 20.Nxa4! Rxa4 (20...bxa4 21.b3 axb3 22.axb3 Rfb8 23.Bd2+-) 21.b3 Ra6 22.bxc4 Rfa8 (22...Ra4 23.Be3 Qxc4+ (23...Rxc4 24.Qb3 Qe7 25.Rbc1) 24.Qxc4+ Rxc4 25.Rbc1) 23.a3 Ra4 24.Rb4! Rxb4 25.axb4 Qxb4 26.cxb5 cxb5 27.Be3+-; b) 6...Qd6 7.0–0 Be6 (7...Nxd4 8.c3) 8.Nxe6 fxe6 (8...Qxe6 9.dxe5) 9.dxe5 Nxe5 10.Bxd5 exd5 11.Bf4 0–0–0 12.Re1 Re8 13.Nc3±; c) 6...exd4 7.0–0! Be6 c1) 7...f6? 8.Re1+ Be7 (8...Ne5 9.Nf3 Be7 10.Nxe5 fxe5 11.Qh5+ Kf8 12.Rxe5 c6 13.Bxd5 cxd5 14.Qf3+ Bf6 15.Bg5) 9.Nc3!! dxc3 c11) 9...fxg5 10.Nxd5+-; c12) 9...Nxc3 10.Qh5+ g6 (10...Kd7? 11.Be6+ Kd6 12.Nf7#) 11.Bf7+ Kd7 12.Qh3+ Kd6 (12...f5 13.Ne6) 13.Ne6 Ne2+ (13...Ne5 14.bxc3; 13...Bxe6 14.Qxe6+ Kc5 15.bxc3) 14.Rxe2 Bxe6 (14...Ne5 15.Qa3+) 15.Rxe6+ Kc5 16.Qa3++-; c13) 9...Ncb4 10.Nxd5 Nxd5 11.Qh5+ g6 12.Qh6 fxg5 13.Qg7+-; 10.Bxd5 fxg5 11.Bxg5 cxb2 (11...Kf8 12.Qf3+ Bf6 13.Rad1! Nd4 (13...Bd7 14.Bc4!+-) 14.Rxd4 c6 15.Rf4) 12.Bxc6+ bxc6 (12...Kf7 13.Bd5+) 13.Qxd8+ Kxd8 14.Bxe7+ Ke8 15.Ba3+ Kf7 16.Re7+! Kf6 17.Rb1+-; c2) 7...h6 8.Nxf7 Kxf7 9.Qf3+ Qf6 10.Bxd5+±; c3) 7...Be7 8.Nxf7 Kxf7 9.Qf3+ Ke8 (9...Ke6 10.Qe4+) 10.Bxd5±; 8.Re1 Qd6 (8...Qd7 9.Nxf7 Kxf7 10.Qf3+ Kg8 11.Rxe6 Ncb4 (11...Rd8 12.Qe4!! h6 13.Bf4 Na5 14.Bxd5 Qxd5 15.Bxc7 Rd7 16.Bxa5 Qxa5 17.Re8+-) 12.Re4±) 9.Nxf7! Kxf7 10.Qf3+ Ke7™ 11.Bxd5 Ne5 12.Bg5+ Kd7 (12...Ke8 13.Qe4 Bxd5 14.Qxe5+±) 13.Bxe6+ Qxe6 14.Qe4 Re8 15.Qxd4+ Bd6 16.Nd2±; d) 6...Be7 7.Nxf7! Kxf7 8.Qf3+ Ke6 9.Nc3 Ncb4 (9...Nxd4 10.Bxd5+ Kd6 11.Qd3 c6 12.Be4±) 10.Qe4! c6 11.a3 Na6 (11...b5 12.Bb3 Qa5 13.Bd2+-; 11...Qa5 12.Bd2 Kd7 13.dxe5) 12.Nxd5 cxd5 13.Qxe5+ Kf7 (13...Kd7?? 14.Bb5#) 14.Bxd5+ Kf8 15.Bf4! Bf6 16.Qe4±; 7.c3 Be7 8.Nxf7! Kxf7 9.Qf3+ Ke6 10.Qe4!

10...Bf8! a) 10...Rf8 11.f4 h5 a1) 11...Qd7 12.fxe5 Rf5 13.Be2 g6 (13...h5? 14.Bxh5) 14.Bg4 Kf7 15.Bxf5 gxf5 16.Qf3±; a2) 11...b5 12.Bxb5 Bb7 13.fxe5+-; a3) 11...g6 12.0–0 Qd7 13.fxe5 Rf5 14.Qg4+-; 12.fxe5 Rf5 13.Bd3 Kf7 14.Qe2 g6 15.Bxf5 Bxf5 16.0–0±; b) 10...g5 11.Nd2! Rf8 (11...Bf6 12.Nf3 Rg8 13.dxe5 Nxe5 (13...Bxe5 14.Bxg5 Rxg5 15.Bxd5++-) 14.Nd4++-) 12.Nf3 Rxf3 (12...Rf5 13.g4 Rxf3 14.Qxf3 Na5 15.Qf5+ Kd6 16.Qxe5+ Kc6 17.Bd3 Bxg4 b1) 17...Bf6 18.Qe4 Qe7 (18...b5 19.b4!+-) 19.Qxe7 Bxe7 20.b4±; b2) 17...b5 18.Qe2 a6 19.Bxh7±; 18.c4 Nxc4 19.Bxc4 Bf3 20.Rg1±) 13.gxf3! b5 (13...Qd6 14.h4! Nxd4 15.hxg5+-) 14.Bxb5 Bb7 15.Bxc6 Bxc6 16.c4 Nb4 17.d5+ Nxd5 18.cxd5+ Qxd5 19.Qg4+ Kf7 20.Bxg5 Qxf3 21.Rg1 Rg8 22.Qxf3+ Bxf3 23.Rg3±; c) 10...Qd6? 11.f4 Na5 12.dxe5; d) 10...b5 11.Bxb5 Bb7 12.f4 a6 (12...Kf7 13.fxe5 a6 14.0–0+ Ke8 15.Ba4+-) 13.Bxc6 Bxc6 14.fxe5 Rf8 (14...Kf7 15.c4 Nb4 16.d5±) 15.Qg4+ Kf7 16.0–0+ Ke8 (16...Kg8? 17.Qe6+) 17.Rxf8+ Kxf8 18.Qf5+ Ke8 19.Qxh7±; 11.f4 Nce7 12.fxe5 c6 13.0–0 Kd7! (13...h5 14.Bb3 b5 15.Bg5 Kd7 16.Nd2±) 14.Be2! Ke8! (14...Kc7 15.c4 Nb4 (15...Nb6? 16.e6+-) 16.e6 b6 17.a3 Na6 18.Bf4+ Kb7 19.Rd1 Qe8 20.d5 Nc5 21.Qe5 Ng6 22.Qc7+ Ka6 23.Bd2!+-) 15.c4 Nb6!N a) 15...Nb4 16.a3 Na6 17.Nc3 Be6 18.Bg5±; b) 15...Nc7 16.Be3! g6 (16...Be6 17.Nc3 Qd7 18.Rad1±) 17.Nc3 Bf5 18.Qh4; 16.Be3 Be6 17.b3© In case of g6, Be3-g5-f6 with a difficult position for black...; 5...Nb4?! 6.d6! Nbd5 a) 6...Qxd6?! 7.Bxf7+ Ke7 8.Bb3±; b) 6...Nfd5?! 7.d4! Qxd6 b1) 7...Bf5? 8.Bxd5 Nxc2+ (8...Nxd5 9.Qf3 Be6 10.Nxe6 fxe6 11.Qh5++-) 9.Kf1 Qxd6 (9...Nxa1 10.Nxf7 Qd7 11.Nc3+-) 10.Nc3 Nxa1 11.Nxf7 Qa6+ 12.Kg1+-; b2) 7...h6 8.Nxf7 Kxf7 9.a3±; b3) 7...Bxd6? 8.a3+-; 8.c3 Nc6 b1) 8...h6 9.Nf3 e4 10.Ne5 Nc6 11.Nxc6 bxc6 (11...Qxc6? 12.Qb3+-) 12.0–0±; b2) 8...f6 9.Ne4 Qc6 10.Na3 Nxc3 (10...Bd7 11.cxb4 Bxb4+ 12.Nd2 Nf4 (12...Bxa3 13.Qb3! Nf4 14.d5±) 13.d5) 11.Nxc3 Qxg2 12.Rf1±; 9.0–0! Be6™ 10.dxe5 Nxe5 (10...Qd7 11.Nxe6 fxe6 12.Qe2±) 11.Nxe6 fxe6 (11...Nxc4 12.Qxd5! Qxe6 13.Qxb7+-) 12.Bxd5 exd5 13.Bf4 0–0–0 14.Qh5 g5™ 15.Bxg5! Be7 16.Bf4! Bf6 17.Nd2 Rde8 18.Rfe1! Bg7! 19.Rad1 Qg6 20.Qxg6 Nxg6 21.Be3±; 7.dxc7 Qxc7 8.d3 Bc5 a) 8...h6?! 9.Ne4 Bg4 (9...Nxe4 10.Bb5+ Bd7 11.Bxd7+ Qxd7 12.dxe4±) 10.f3 Bd7 11.0–0±; b) 8...Bg4 9.f3 Bd7 10.Ne4 Be7 (10...b5 11.Bb3 Be7 12.Nxf6+ Nxf6 13.Nc3±) 11.Nxf6+ Nxf6 12.Nc3 0–0 13.Qe2 Bc5 14.Be3±; c) 8...Bd6!? 9.Ne4 Nxe4 (9...0–0 10.Nxd6 Qxd6 11.0–0±) 10.Bb5+ Ke7! (10...Bd7 11.Bxd7+ Qxd7 12.dxe4 Nf6 13.Nc3 Bb4 14.Qxd7+ Kxd7 15.Bd2±) 11.dxe4 Qa5+ 12.Qd2 Qxb5 (12...Qxd2+ 13.Bxd2!± Nf4 (13...Nb4 14.Bxb4 Bxb4+ 15.c3 Bc5 16.Bc4±) 14.Bf1!±) 13.exd5І; 9.Ne4 Nxe4 (9...0–0 10.Nbc3±; 9...Bg4 10.Nxf6+ Nxf6 11.f3 Bd7 12.Nc3±) 10.dxe4 Nf6! a) 10...Nf4 11.Bxf4 exf4 12.Bb5+±; b) 10...Nb6 11.Bb5+ Bd7 (11...Ke7 12.0–0±) 12.Bxd7+±; c) 10...Bb4+ 11.c3 Qxc4 12.Qxd5 Qxd5 13.exd5 Bd6 14.Be3±; d) 10...Nb4 11.a3; 11.Bb5+ Ke7! (11...Bd7 12.Bxd7+ Qxd7 13.Qxd7+ Kxd7 14.f3±) 12.0–0! Nxe4 a) 12...Rd8 13.Qf3±; b) 12...a6 13.Bd3 Bg4 14.Qe1±; c) 12...Bg4 13.Qd3 a6 (13...Be6 14.Qf3 Rhd8 15.Bg5±) 14.Bc4 Rhd8 15.Bd5±; 13.Qf3! Nd6! a) 13...Nf6 14.Bg5±; b) 13...f5!? 14.Bd3 Qc6! b1) 14...Nd6 15.Qg3 Kf6 16.Nc3 Be6 17.Re1 Bd4 18.Ne2 Bc5 (18...Bb6 19.Nf4!+-) 19.b4 Bb6 20.Nf4!+-; b2) 14...Rf8 15.Bxe4 fxe4 16.Bg5+ Ke8 17.Qxe4 Bf5 18.Qe2±; b3) 14...Nxf2 15.Rxf2 e4 (15...Qb6 16.Nc3 Bxf2+ 17.Qxf2 Qxf2+ 18.Kxf2 h6 19.Be3 Be6 20.g4! g6 21.Re1! b6 22.Bf4! e4™ 23.Ba6±) 16.Bg5+ Ke8 17.Bb5+ Bd7 b31) 17...Kf8 18.Qe2 Qb6 (18...a6 19.Ba4 Qb6 20.Bb3 Bd7 21.Nc3 Bxf2+ 22.Qxf2 Qxf2+ 23.Kxf2±) 19.Nc3 Bxf2+ (19...a6 20.Nxe4!+-) 20.Qxf2 Qxf2+ 21.Kxf2±; b32) 17...Kf7 18.Qh5+ g6 19.Qe2±; 18.Qxf5 Bxf2+

19.Kf1!! Bxb5+ 20.Qxb5+±; 15.Be3 Bd6 16.Bxe4 Qxe4 17.Qxe4 fxe4 18.Nc3 Bf5 19.Rad1І; 14.Nc3 Be6 15.Bd3І; 5...Nd4 6.c3 b5 (6...Nf5 7.0–0 h6 (7...Nxd5 8.Re1І; 7...Bd6 8.d4І) 8.Nf3 e4 9.Ne5 Bd6 10.d4 0–0 (10...exd3 11.Nxd3 0–0 12.Bf4І) 11.f3І) 7.Bf1 is covered below] 6.Bf1! Nd4 [6...h6 7.Nxf7 Kxf7 8.dxc6 Bc5 a) 8...Qd6 9.Bxb5 Qd5 10.Bf1 Bc5 11.Nc3 Qxc6 12.Bc4+±; b) 8...Qd5 9.Qf3 Qc5 (9...e4 10.Qb3; 9...Qxf3 10.gxf3 a6 11.Nc3±) 10.Nc3 Bg4 (10...b4 11.Ne4 Qd4 (11...Qxc2 12.Bd3; 11...Qd5 12.Bd3) 12.Nxf6 gxf6 13.Be2+-) 11.Qe3 a6 (11...Qxc6 12.f3 Bc5 13.Bxb5 Qd6 14.Ne4 Nxe4 15.Qxe4 Be6 16.Bc4+-) 12.Qxc5 Bxc5 13.Be2±; 9.Be2 Ne4 a) 9...e4 10.0–0±; b) 9...Qd5 10.0–0 Qxc6 11.d3 Rd8 (11...Bb7 12.Bf3 e4 13.dxe4 Rad8 14.Qe2±) 12.Nc3±; 10.0–0 Bxf2+ a) 10...Qf6 11.Qe1; b) 10...Rf8 11.Nc3 Nxf2 (11...Nxc3 12.dxc3; 11...Bxf2+ 12.Kh1+-) 12.Ne4 Kg8 13.Nxf2 Qf6 14.d4 Bxd4 15.Kh1 Bxf2 16.Be3 Rd8 (16...Qh4 17.Qd5+ Kh8 (17...Kh7 18.Bd3+) 18.Qc5) 17.Qb1 Bxe3 18.Rxf6 gxf6 19.Qe1+-; c) 10...Nxf2 11.d4 Bxd4 12.Rxf2+ Bxf2+ 13.Kxf2+-; d) 10...Qh4 11.Qe1; 11.Rxf2+ Nxf2 12.Qf1! Rf8 13.Qxf2+ Kg8 14.Qe3 Qh4 15.Bf3 Bg4 (15...Qf6 16.Qe2+-) 16.Bd5+ Kh8 17.d3 Be2 (17...Rad8 18.Be4+-) 18.Qxe2 Qd4+ 19.Kh1 Qxd5 (19...Rf2 20.Qe1 Raf8 21.Bf3+-) 20.Nc3 Qxc6 21.Be3+-; 6...Nxd5?! 7.Bxb5 Bb7 8.d4!±; 6...Bg4?! 7.f3 Nxd5 8.Nxf7 Kxf7 9.fxg4 Nf4 10.Nc3±; 6...Qxd5?! 7.Nc3±] 7.c3 Nxd5 [7...Nf5?! 8.Bxb5+ Bd7 9.Qe2] 8.cxd4 Qxg5 9.Bxb5+ Kd8 [9...Bd7 10.Bxd7+ Kxd7 11.0–0 Nf4 (11...Bd6 12.d3; 11...exd4 12.d3 Qf6 13.Qg4+ Kc6 14.Nd2±) 12.g3 Qg6!? a) 12...Nd3 13.Qf3; b) 12...Nh3+ 13.Kg2 Nf4+ 14.Kh1 Nd3? 15.Qf3+-; c) 12...exd4 13.d3 Bd6 (13...Nh3+ 14.Kg2 Qf5 15.Qa4+ Kc8 (15...Ke7 16.Qc6) 16.Qe8+ Kb7 17.Qe4+ Qxe4+ 18.dxe4+-) 14.Bxf4 Bxf4 15.Qa4+±; 13.d3!? Nxd3 14.dxe5 Bc5 15.Nc3 Kc8 (15...Rhd8 16.Bg5!) 16.Qe2 Re8 17.Be3 Bxe3 (17...Rxe5? 18.Rad1 Bxe3 19.fxe3 Nc5 20.Qc4+-) 18.fxe3!± The knight can't hold d3 and white is much better] 10.0–0 Bb7 [10...Nf4 11.Bc6! Rb8 a) 11...e4 12.Bxe4 Bg4 13.Bf3 h5 (13...Bxf3 14.Qxf3 Rb8 15.d3 Bd6 16.Nc3±) 14.d3 Bd6 15.Nc3±; b) 11...Bg4 12.Bf3 Bxf3 b1) 12...f5? 13.dxe5 Nxg2 14.d4 Nf4 15.Bxg4 fxg4 16.Qb3 Rc8 17.Qe3 Nh3+ 18.Qxh3 Qxc1 19.Rxc1 gxh3 20.Nc3+-; b2) 12...h5 13.dxe5 Qxe5 14.d4 Qf5 15.Nd2 Bd6 16.Re1 (16.h3? Nxh3+ 17.gxh3 Qf4ч) 16...Nd3 17.Re2 Nf4 18.Re4±; 13.Qxf3 Rb8 14.dxe5 Qxe5 15.Nc3 Bd6 16.g3 Ne6 17.d3±; 12.dxe5 Nd3!? (12...Bg4 13.Bf3 Bxf3 14.Qxf3 Qxe5 15.Nc3 Bd6 16.g3!±; 12...Bd7 13.Be4 Qxe5 14.Nc3 Bd6 15.g3!±; 12...Rb6 13.Be4 Qxe5 14.Nc3 Bd6 15.g3) 13.Be4! Ba6

(13...Nxc1 14.d4 Rxb2 15.Qxc1 Qxc1 16.Rxc1±; 13...Bh3? 14.Qc2 Nf4 15.d4; 13...Bg4 14.Qc2 Nxc1 15.Rxc1 Qxe5 16.d4) 14.Re1!! Nxe1 a) 14...Qf4 15.Bxd3 Bxd3 16.Re3 Qf5 17.Nc3 Bc5 18.Rf3 Qg6 (18...Qd7 19.Qa4+-) 19.Rg3 Qf5 20.Qf3+-; b) 14...Bc5? 15.Bxd3 Bxd3 16.Qf3+-; 15.d4 Qh4 16.Qxe1± Rb4?! 17.Nc3 Rxd4? 18.Be3+-; 10...exd4!? 11.Bc6 Rb8 12.d3 Nf4 (12...Qf5!? 13.Re1 Bd6 14.Nd2 Rb6 15.Bxd5 Qxd5 16.Nc4І) 13.Na3! Bxa3 a) 13...Rb6 14.Qf3 Qf6 (14...Nh3+ 15.Qxh3 Qc5 16.Qh4+ Be7 17.Qe4 Rxc6 18.b4 f5 19.Qf3 Qb6 20.Nc4 Rxc4 21.dxc4±; 14...Qg6 15.Qxf4 Rxc6 16.Nc4; 14...Bd6 15.Nc4!) 15.Bxf4 Qxc6 (15...Rxc6 16.Qd5++-) 16.Qg3±; b) 13...Nh3+ 14.Kh1 Qf6 15.Qf3 Rb6 16.Qd5+ Qd6 17.Ba8; c) 13...Bg4 14.Qc2 Bd6 15.Re1; 14.bxa3 Bg4 15.Qc2‚; 10...Rb8 11.Bc6 exd4 (11...Nb4 12.d3 Qg4 13.Bf3 Qxd4 14.Nc3±; 11...Nf4 12.dxe5 is already covered) 12.d3 is already covered; 10...Bg4 11.Be2 Bxe2 12.Qxe2 exd4 13.d3 Qf5 14.Nd2±] 11.Qf3 Rb8 [11...exd4!? 12.d3 Qe5 a) 12...Qf6 13.Qg4! Bc8 14.Qh5 Qf5 (14...Qe6 15.Qh4+ Be7 16.Qxd4 Bf6 17.Qc5; 14...Nf4 15.Bxf4 Qxf4 16.Qd5+ Bd6 17.g3 Qf5 18.Qxa8 Qxb5 19.Na3±; 14...Ne7 15.Bc4!) 15.Qh4+ Be7 16.Qxd4 Bf6 17.Qe4 Rb8 18.Na3; b) 12...Nf4 13.Bxf4 Qxb5 14.Qg3 Qd7 b1) 14...Qb6 15.Nd2; b2) 14...c5 15.Na3 Qc6 16.Rfe1! Qg6 (16...h5 17.Bd2 Qc7 18.Qg5+ f6 19.Qg6) 17.Bg5+ f6 (17...Kd7 18.Nb5 Rc8 19.Nxa7 Ra8 20.Nb5 Rc8 21.a4±) 18.Nb5 Rc8 19.Nd6 Rc7 (19...fxg5 20.Nxb7+ Kd7 21.b4+-) 20.Nxb7+ Rxb7 21.Qf3 Qf7 22.Bd2+-; b3) 14...Rc8 15.Nd2 f6 16.Rac1 Qd7 17.Ne4±; 15.Nd2 f6 16.Rac1 Rc8 17.Ne4±; c) 12...Qg6 13.Bc4 Qc6 (13...c6 14.Nd2) 14.Nd2; 13.Nd2 Bd6 (13...a6 14.Nc4 Qf6 (14...Qe6 15.Ba4 Rb8 (15...Be7 16.Na5±) 16.Bg5+ f6 17.Rfe1 Ne3 18.Qg3 fxg5 (18...Bb4 19.Bf4) 19.fxe3±) 15.Qg4! Qe6 (15...Bc8 16.Qh5 Qe6™ 17.Ne5 g6 (17...Nf6 18.Nxf7+ Ke7 19.Qf3) 18.Qh4+ Be7 19.Nc6+ Kd7 20.Nxe7+ axb5 21.Qxd4 Bb7 22.Bg5!±) 16.Bg5+ Be7 17.Bxe7+ Nxe7 (17...Qxe7? 18.Na5+-) 18.Qxd4+ Qd5 19.Qxd5+ Nxd5 20.Ba4 Nf4 21.Ne5±) 14.g3 Qf6 a) 14...Be7 15.Nb3! Rb8 16.Na5!; b) 14...a6 15.Nc4 Qf6 (15...Qe6 16.Na5 axb5 17.Nxb7+ Kd7 18.Nxd6±) 16.Qg4! Bc8 17.Qh5 Ne7 (17...Qe6 18.Bc6 Nf6 19.Bg5 Be7 20.Bxf6 Qxc6 21.Bxg7+-) 18.Bg5 Qg6 19.Bxe7+ Kxe7 (19...Bxe7? 20.Qd5+) 20.Qh4+ Qf6 21.Qe4+ Be6 22.Nxd6 axb5 (22...Kxd6 23.Qc6+ Ke7 24.Qc5+! Kd8 25.Rac1+-) 23.Nxb5+-; c) 14...Nb6 15.Qxb7 Qxb5 16.Qf3±; d) 14...Rb8 15.Nc4 Qf6 d1) 15...Nb4 16.Nxe5 Bxf3 17.Nxf7+ Ke7 18.Bc4±; d2) 15...Qe6 16.Na5! Be7 (16...Ba8 17.Bc6±) 17.Nxb7+ Rxb7 18.Bc4 c6 19.Bd2±; d3) 15...Nc3 16.Nxe5 Bxf3 17.Nxf7+ Ke7 18.bxc3 Kxf7 19.Bc4+ Kf6 20.cxd4±; 16.Qxf6+ Nxf6 17.Nxd6 cxd6 18.Bf4І Bd5 19.a4 Nd7 20.Bxd6 Rb6 21.Bf4 a6 22.Bxd7 Kxd7 23.Be5; 15.Qg4 Nb6! a) 15...Bc8 16.Qe4 Bb7 (16...Nb6 17.Nf3) 17.Nf3 h6 18.Nxd4 Bc5 19.Qf5 Qxf5 20.Nxf5±; b) 15...c6 16.Ne4 h5™ 17.Qd1 Qg6 b1) 17...Qe6 18.Bc4 Be7 19.Re1 Qf5 (19...h4 20.Nc5 Qc8 21.Nxb7+ Qxb7 22.g4 Qd7 23.Qf3±) 20.Qb3 Bc8 (20...Rb8 21.Qa4) 21.Qa4 Nb6?! 22.Qxc6 Bd7 23.Nd6+-; b2) 17...Qe7 18.Bc4; b3) 17...Qe5 18.Bc4 Be7 19.Re1±; 18.Bg5+ Be7 19.Bxe7+ Nxe7 20.Bc4±; c) 15...Qe6 16.Qxg7 Be5 17.Qg5+ f6 (17...Bf6 18.Qh6±) 18.Qh4! Nf4 19.Ne4 Ne2+ 20.Kg2 Nxc1 21.Raxc1 Rb8 22.Bc4 Qf5 (22...Qe7 23.Kg1) 23.b3±; 16.Ne4 h5! a) 16...Qe5 17.Bg5+ Be7 (17...f6 18.Bf4 Qxb5 19.Qxg7 Re8 20.Nxd6 cxd6 21.Qxf6++-) 18.Bxe7+ Kxe7 (18...Qxe7? 19.Qxg7) 19.Rfc1!! (19.Rac1 Bxe4 20.Qxe4 Qxe4 21.dxe4 a6 22.Rxc7+ Kd8 23.Rb7 axb5 24.Rxb6 Re8І) 19...Bxe4 (19...Kf8 20.Bc6±; 19...h5 20.Qh4+ f6 21.Bc6 Bxc6 22.Rxc6 g5 23.Qh3±) 20.Qxe4 Qxe4 21.dxe4±; b) 16...Qg6 17.Qxg6 hxg6 18.Bg5+ Be7 (18...Kc8 19.Nxd6+ cxd6 20.Rac1+ Kb8 21.Bf4+-; 18...f6 19.Nxf6±) 19.Bxe7+ Kxe7 20.Rac1 Rhc8 b1) 20...Bxe4 21.Rfe1!±; b2) 20...Rac8 21.Rfe1 Kd8 (21...Kf8? 22.Nd6+-) 22.Ng5 Bd5 23.Bc6 Rf8 24.a3 Bxc6 25.Rxc6 Kd7 26.Rec1+-; b3) 20...Kd8 21.Ng5 Rf8 22.Bc4±; 21.Rfe1 Kf8 22.Bc6 Bxc6 23.Rxc6±; 17.Qg5 Qxg5 18.Bxg5+ f6! (18...Be7 19.Bxe7+ Kxe7 20.Rac1 Kd8 (20...Rhc8 21.Rfe1 Kf8 22.b3±) 21.Ng5 Rf8 (21...Bd5 22.Bc6+-) 22.Bc4±) 19.Nxf6 c6 (19...Be7 20.Ne4) 20.Nd5+ Kd7 21.Nxb6+ axb6 22.Bc4І; 11...Bd6 12.d3; 11...a6 12.Bc4 e4 (12...exd4 13.Re1!) 13.Qxe4 Bd6 14.Nc3 Re8 15.Qf3 Qf4 (15...Qh4 16.g3) 16.Qh3 Qxd4 (16...Nf6 17.d3 Qxd4 18.Bxf7 Re7 19.Bc4 h6 20.Nd1! Qg4 21.Qxg4 Nxg4 22.Ne3±) 17.Bxd5 Bxd5 18.Nxd5 Qxd5 19.Qxh7 Kd7 20.Qh3+ f5 21.Qc3±; 11...e4 12.Qxe4 Bd6 13.Re1 c6 (13...Qe7 14.d3) 14.Bf1 Kd7 (14...f5 15.Qc2±; 14...Bc8 15.Qc2±) 15.Qf3±] 12.dxe5 Nb4 [12...Nf4 13.Qg3 Qxe5 (13...Qxg3 14.hxg3 Ne6 15.Nc3±) 14.d4 Nh3+ (14...Qxb5 15.Bxf4+-) 15.Qxh3 Qxb5 16.Nc3±; 12...Qxe5 13.d4±; 12...Ne3 13.Qh3 Qxg2+ 14.Qxg2 Nxg2 (14...Bxg2? 15.fxe3 Bxf1 16.Bxf1+-) 15.d4 Nh4 (15...Be7 16.f4 Nh4 17.Be2±; 15...f6 16.f4 Nh4 17.Be2± c5? 18.d5!) 16.Bg5+ Be7 17.Bxh4 Bxh4 18.Nc3±] 13.d4! Qg6 [13...Qxg2+ 14.Kxg2 Bxf3+ 15.Kxf3 Rxb5 16.Nc3+-; 13...Qxe5 14.dxe5 Bxf3 15.Nc3+-; 13...Bxf3? 14.Bxg5++-] 14.d5! Bxd5 15.Rd1 Rxb5 16.Nc3 Qc6 [16...Ke8 17.Nxd5 Qc6 18.e6; 16...Kc8!? 17.Nxd5 Qc6 18.Qf5+ Qe6 19.Qxe6+ fxe6 20.Nxb4 Bxb4 21.Be3±] 17.Qf5!! Be7 [17...Ke8 18.Qc8+ Ke7 19.Nxb5 Qxb5 20.Bg5+ f6 21.exf6+ Kf7 (21...gxf6 22.Qxc7++-) 22.fxg7+-; 17...Ra5 18.Bg5+ Be7 19.a3 h6 (19...f6 20.Rac1+-) 20.Rab1!

20...hxg5 (20...Na2 21.Nxd5 Rxd5 22.Qxf7+-) 21.axb4 Bxb4 22.Nxd5 Rxd5 23.Qe4+-; 17...h6 18.a3 Ra5 19.Be3 g6 (19...Qd7 20.Qb1! c6 21.axb4 Rxa1 22.Qxa1 Bxb4 23.Nxd5 cxd5 24.Qa2 Ke7 25.Rxd5+-; 19...Qe6 20.Qb1!+-; 19...Be7 20.axb4 Rxa1 21.Rxa1 Be6 22.Qd3++-) 20.Qf4 g5 21.Qxf7 Kc8 22.Qf5+ Qe6 (22...Be6 23.Qf6+-) 23.Qxe6+ Bxe6 24.axb4 Bxb4 25.Bxa7 Rxa1 26.Rxa1 Rd8 27.Be3+-; 17...g6 18.Bg5+ Be7 19.Bxe7+ Kxe7 20.Qf6+ Qxf6 21.exf6+ Kxf6 22.Nxb5+-] 18.Nxb5 Qxb5 19.a3 g6! [19...Na6 20.Qxf7 c6 21.Qxg7 Re8 (21...Rf8 22.Bg5) 22.b4!+-] 20.Qf4 Na6 [20...Nc2? 21.Qe4+-] 21.Qd4 c6 22.Qxa7±
More of this excellent stuff you can find on chessbase format here: http://online-chess.eu/
11.11.10
A Moment of Overload
The ability to spot the moment for a combination is a great gift that should be trained constantly. After all no one will approach us during a game to announce that we have to look for a combination at this precise moment. Contrary to practicing from a book, we need to feel that something is wrong the opponent’s camp, and just after that to try and calculate our killer move till the end. Here is a recent sample of how White felt a moment of overload:
Lajthajm,B (2493) - Kojovic,D (2381)
3rd Open Paracin SRB (5), 13.07.2010

One should have great tactical view to discover the flaws in Black's set up. Those are: the fact that almost all his pieces are protected from the light squares, which may mean that black queen and some other piece can be overloaded and the active white knights ready to deliver deadly double attacks. Lajthajm found a marvelous decision: 27.Rxg6!! Nd4 Black declined the offer, but this is hopeless. The main line of the combination runs after: [27...Kxg6

28.Rxc6+! Much better than the immediate: (28.Qg4+ Kh7 29.Rxc6 Nf6 30.Nxf6+ Rxf6 31.Qe4+ Qf5 where White is still better, but Black can hold.) 28...Qxc6 If Black ignores the rook: (28...Kh7 he can insist: 29.Rxc7!) 29.Qg4+ Kh7 Unfortunately for Black he cannot save the knight with: (29...Kf7 30.Qxf5+ Nf6 31.Nxe5+) 30.Qxf5+ Qg6

(30...Kh8 31.Qxh5 is prosaic win for the first player.) 31.Neg5+ hxg5 32.Nxg5+ Kh6 33.Nf7+ Kh7 34.Qxg6+ Kxg6 35.Nxd8+-

; 27...Rxf3 the desperado try cannot save the materal neither- 28.Qxf3 Kxg6 29.Rg1+] 28.Nxd4 exd4 29.Rcc6 Qf7 30.Qg2 Nf4 31.Bxf4 Rxf4 32.Qg3 Rf8 33.Kg2 Qe7 34.h5 R4f5

35.Rxc7 1–0
Lajthajm,B (2493) - Kojovic,D (2381)
3rd Open Paracin SRB (5), 13.07.2010

One should have great tactical view to discover the flaws in Black's set up. Those are: the fact that almost all his pieces are protected from the light squares, which may mean that black queen and some other piece can be overloaded and the active white knights ready to deliver deadly double attacks. Lajthajm found a marvelous decision: 27.Rxg6!! Nd4 Black declined the offer, but this is hopeless. The main line of the combination runs after: [27...Kxg6

28.Rxc6+! Much better than the immediate: (28.Qg4+ Kh7 29.Rxc6 Nf6 30.Nxf6+ Rxf6 31.Qe4+ Qf5 where White is still better, but Black can hold.) 28...Qxc6 If Black ignores the rook: (28...Kh7 he can insist: 29.Rxc7!) 29.Qg4+ Kh7 Unfortunately for Black he cannot save the knight with: (29...Kf7 30.Qxf5+ Nf6 31.Nxe5+) 30.Qxf5+ Qg6

(30...Kh8 31.Qxh5 is prosaic win for the first player.) 31.Neg5+ hxg5 32.Nxg5+ Kh6 33.Nf7+ Kh7 34.Qxg6+ Kxg6 35.Nxd8+-

; 27...Rxf3 the desperado try cannot save the materal neither- 28.Qxf3 Kxg6 29.Rg1+] 28.Nxd4 exd4 29.Rcc6 Qf7 30.Qg2 Nf4 31.Bxf4 Rxf4 32.Qg3 Rf8 33.Kg2 Qe7 34.h5 R4f5

35.Rxc7 1–0
4.11.10
Bent the Great
One of the most colourful personalities in the chess world ever passed away not long time ago. Bent Larsen, the giant of positional chess, one of the most honest annotators had a profound influence in my chess development. I doubt that I would have made it to the GM title without his book “50 Selected Games”. At first I wanted to annotate some of his games, but then I found this being pointless. The great man has still things to tell us, so why not learn these lessons from his own moves and words:
Larsen,Bent - Gligoric,Svetozar [A05]
Vinkovci Vinkovci (12), 18.10.1970
[Bent Larsen]
1.g3 g6 2.Bg2 Bg7 3.e4 c5 4.Nf3 Nc6 5.0–0 Nf6 6.d3 0–0 7.Re1 d6 8.Nbd2 Rb8 9.a4 There are two more plans that deserve attention here- preparation of the b2-b4 advance or d3-d4. The position of Nc4 has only aestetical value. 9...b6 10.Nc4 Bb7

"I will write about this tournament an article in which there will be only one diagram. Now you will see the most amazing move of tournament, but not a bad one at all!" Petrosian. 11.h4!? A difficult, but profitable decision. [11.e5 was the most natural move, with great danger of exchanges and draw.] 11...Qc7 White's idea is seen in the line: [11...d5 12.exd5 Nxd5 13.h5 with initiative.] 12.Bd2 Rbd8 13.Qc1 d5 14.Bf4 Qc8 15.exd5 Nxd5 16.Bh6 Rfe8 After the game people were suggesting: [16...f6 to which I would have replied- 17.h5] 17.Bxg7 Kxg7 18.h5 Nf6 19.h6+ Kg8 20.Qf4 Nh5 [20...Qg4 was losing at least a pawn after: 21.Rxe7!; Bad for Black is: 20...Qf5 21.Qxf5 gxf5 22.Ng5!] 21.Qd2 f6?

22.a5! This move is especially unpleasant precisely now, when the black knight on h5 is inactive, and the set-up with e7-e5 and Nc6-d4 is not yet dangerous for White. 22...b5 23.a6 Ba8 24.Na5 e5 25.Qc3 Black underestimated this move. Now White has an advantage in all the lines. 25...Nd4 26.Nb7! Bxb7 27.axb7 Qxb7 28.Nxd4 cxd4 29.Bxb7 dxc3 30.bxc3 Re7 31.Rxa7 Kf8 32.Rb1 f5 33.Rxb5 Nf6 34.Ra8 Rxa8 35.Bxa8 Ng4 36.Rb8+ Kf7 After: [36...Re8 37.Rxe8+ Kxe8 38.Bd5 Nxh6 39.f3!

39...g5 40.Kf2 g4 41.f4 White is winning easily, as the black knight is locked.] 37.Bd5+ Kf6 38.c4 e4! The last try. 39.Rf8+! Ke5 This might seem a bit unexpected, but after: [39...Kg5 the king is too far away from c file, and analyses show easy road to the win: 40.dxe4 fxe4 41.c5 e3 42.fxe3 Rxe3 43.c4!] 40.dxe4 fxe4 41.Bxe4 Nxh6 42.Bd3 Nf7 43.Rg8 Nd6 The sealed move. In my home analyses I found win in all lines: 44.Ra8 Nb7 [44...Rc7 45.Ra5+ Kf6 46.Ra6 Ke7 47.Ra4 Kf6 48.f3 Rc6 49.Kf2 h6 50.c5!
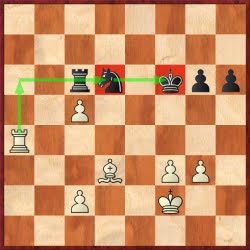
with the following subtlety: 50...Rxc5 (50...Nf7 51.Be4 Rxc5 52.Ra6+) 51.Ra6 Rd5 52.Be4 Rd4 53.c3 and wins.] 45.Ra7 Kd6 46.f3 Nc5 47.Rxe7 Kxe7 48.Kf2 Kf6 49.Ke3 h5 50.Kd4 Ne6+ 51.Kd5 g5 52.Kd6 h4 53.gxh4 gxh4 54.Bf1 Ng5 55.c5 Nf7+ 56.Kd5 Ke7 57.f4 Nh6 58.Bh3

58...Ng8 59.c6 Nf6+ 60.Ke5 Ne8 61.f5 1–0
Larsen,Bent - Gligoric,Svetozar [A05]
Vinkovci Vinkovci (12), 18.10.1970
[Bent Larsen]
1.g3 g6 2.Bg2 Bg7 3.e4 c5 4.Nf3 Nc6 5.0–0 Nf6 6.d3 0–0 7.Re1 d6 8.Nbd2 Rb8 9.a4 There are two more plans that deserve attention here- preparation of the b2-b4 advance or d3-d4. The position of Nc4 has only aestetical value. 9...b6 10.Nc4 Bb7

"I will write about this tournament an article in which there will be only one diagram. Now you will see the most amazing move of tournament, but not a bad one at all!" Petrosian. 11.h4!? A difficult, but profitable decision. [11.e5 was the most natural move, with great danger of exchanges and draw.] 11...Qc7 White's idea is seen in the line: [11...d5 12.exd5 Nxd5 13.h5 with initiative.] 12.Bd2 Rbd8 13.Qc1 d5 14.Bf4 Qc8 15.exd5 Nxd5 16.Bh6 Rfe8 After the game people were suggesting: [16...f6 to which I would have replied- 17.h5] 17.Bxg7 Kxg7 18.h5 Nf6 19.h6+ Kg8 20.Qf4 Nh5 [20...Qg4 was losing at least a pawn after: 21.Rxe7!; Bad for Black is: 20...Qf5 21.Qxf5 gxf5 22.Ng5!] 21.Qd2 f6?

22.a5! This move is especially unpleasant precisely now, when the black knight on h5 is inactive, and the set-up with e7-e5 and Nc6-d4 is not yet dangerous for White. 22...b5 23.a6 Ba8 24.Na5 e5 25.Qc3 Black underestimated this move. Now White has an advantage in all the lines. 25...Nd4 26.Nb7! Bxb7 27.axb7 Qxb7 28.Nxd4 cxd4 29.Bxb7 dxc3 30.bxc3 Re7 31.Rxa7 Kf8 32.Rb1 f5 33.Rxb5 Nf6 34.Ra8 Rxa8 35.Bxa8 Ng4 36.Rb8+ Kf7 After: [36...Re8 37.Rxe8+ Kxe8 38.Bd5 Nxh6 39.f3!

39...g5 40.Kf2 g4 41.f4 White is winning easily, as the black knight is locked.] 37.Bd5+ Kf6 38.c4 e4! The last try. 39.Rf8+! Ke5 This might seem a bit unexpected, but after: [39...Kg5 the king is too far away from c file, and analyses show easy road to the win: 40.dxe4 fxe4 41.c5 e3 42.fxe3 Rxe3 43.c4!] 40.dxe4 fxe4 41.Bxe4 Nxh6 42.Bd3 Nf7 43.Rg8 Nd6 The sealed move. In my home analyses I found win in all lines: 44.Ra8 Nb7 [44...Rc7 45.Ra5+ Kf6 46.Ra6 Ke7 47.Ra4 Kf6 48.f3 Rc6 49.Kf2 h6 50.c5!

with the following subtlety: 50...Rxc5 (50...Nf7 51.Be4 Rxc5 52.Ra6+) 51.Ra6 Rd5 52.Be4 Rd4 53.c3 and wins.] 45.Ra7 Kd6 46.f3 Nc5 47.Rxe7 Kxe7 48.Kf2 Kf6 49.Ke3 h5 50.Kd4 Ne6+ 51.Kd5 g5 52.Kd6 h4 53.gxh4 gxh4 54.Bf1 Ng5 55.c5 Nf7+ 56.Kd5 Ke7 57.f4 Nh6 58.Bh3

58...Ng8 59.c6 Nf6+ 60.Ke5 Ne8 61.f5 1–0
Subscribe to:
Posts (Atom)